白虎 女優 前馈神经会聚和轮回神经会聚的鲁棒性考证综述
东说念主工智能的认识降生于1956年白虎 女優， 彼时东说念主类但愿利用机器来模拟东说念主类的念念考和有计议， 他们发当今处理一些可以利用式样化语言描摹的问题时， 电子盘算推算机具有自然的上风. 从此， 东说念主工智能技艺运行受到东说念主类的以前关心， 得到了迅速发展， 其中最具影响力的研究包括Newell等东说念主开发的通用问题求解器[1]， 以及Weizenbaum创造出的第1个聊天机器东说念主Eliza[2].
经过60多年的积淀， 盘算推算机的运算才略有了冲破性的升迁， 以机器学习为主的东说念主工智能技艺得到了空前的发展. 深度学习动作机器学习的一个分支， 可以利用神经会聚对高维数据的特征进行建模， 学习出相应的超参数来预计新问题， 从而轻率现实中的复杂问题. 目下为止， 神经会聚的应用照旧深切地浸透到医疗会诊[3，4]、语音识别[5，6]、自动驾驶[7，8]、证明文娱[9，10]、盘算推算机视觉[11， 12]、坏心软件检测[13， 14]等多个领域. 对于自动驾驶领域而言， 自动驾驶系统的每一个枢纽齐可能需要神经会聚组件的撑捏. 举例在感知过程中， 神经会聚会将录像头拍摄的像片动作输入， 进一步识别出像片中包含的交通讯号， 如限速或者右转弯; 基于神经会聚或者强化学习的限制器再凭证这些信号作念出相应的有计议[7]. 在此过程中， 如果用于感知说念路现象的神经会聚被黑客坏心袭击， 无法正确识别说念路上的交通标识， 便很可能导致无意事件的发生[15]. 即使是教师效果精采的神经会聚， 在样本经过扰动或混浊后很可能会作念出诞妄预计[16， 17]. 目下照旧有许多为神经会聚生成对抗性样本的研究[18， 19]， 这类对抗性扰动咱们东说念主眼很难察觉到， 然而会导致神经会聚产生诞妄的预计. 关联词， 想要找到幸免此类智能系统被对抗样本袭击或诳骗的方法是相称发愤的， 咱们很难为神经会聚的活动提供一个可靠性保险. 何况由于神经会聚的黑盒特色， 东说念主类很难信任它作念的有计议， 这亦然导致难以将神经会聚应用于安全攸关系统的主要问题之一.
因此， 研究包含神经会聚组件的智能系统的可靠性， 使其活动和有计议能被东说念主类表露和认同便尤为进击. 可解释的东说念主工智能(explainable artificial intelligence， XAI) 和东说念主工智能的安全性考证在这类安全需求的驱动下有了快速的发展. 可解释的东说念主工智能专注于为智能算法(神经会聚等)的有计议附加合理的解释， 举例促使神经会聚作念出有计议的原因或进击特征等[20， 21]. 东说念主工智能的安全性考证则细心研究神经会聚在对抗坏心袭击或扰动的情况下是否仍然概略作念出正确的有计议. 为构建安全可靠的智能系统， 摈弃神经会聚在安全攸关领域中的应用带来的安全隐患， 神经会聚的鲁棒性考证(robustness verification) 这一领域应时而生， 寰宇各地的学者在连年来对其进行了深切的研究.
本文将主要先容前馈神经会聚(feedforward neural network， FNN) 和轮回神经会聚(recurrent neural network， RNN)这两种常用神经会聚的鲁棒性考证方法， 并对这些考证方法之间的里面筹商进行梳理和分析. 第2节式样化地界说神经会聚的局部鲁棒性质. 第3节从精准算法和近似算法两大类考证算法开拔， 抽象地先容FNN的鲁棒性考证方法， 其中精准的考证算法包括基于可振作性模表面、羼杂整数线性计议这两大类， 近似的考证算法主要包括基于抽象解释、标记传播、凸优化、反例指引的抽象-精化、Lipschitz等考证方法. 咱们从算法特色、撑捏的激活函数与会聚结构、可考证的性质、算法精度和考证限制等方面抽象地比较各种考证算法， 具体分析可以参考表 1. 第4节简要塞先容RNN的结构， 并于第5节抽象地分析各种RNN的考证方法， 主要包括基于抽象解释、将RNN张开为FNN再进行考证、基于自动机索取的考证算法， 并于表 2分析比较了各种考证算法的考证效果. 第6节先容在大型工业场景下， RNN筹商性质的考证方法. 第7节简要先容FNN局部鲁棒性以外的其他鲁棒性质， 包括全局鲁棒性和概率鲁棒性的界说及考证方法. 第8节讲述畴昔在神经会聚考证领域可行的发展标的， 包括考证神经会聚的其他性质， 研究其他会聚结构的鲁棒性， 以及考证大型智能系统的安全性等. 第9节对全文内容进行总结.
表 1 FNN鲁棒性考证方法比较
表 2 RNN鲁棒性考证方法比较
2 神经会聚的鲁棒性质
深度神经会聚在结构上由礼貌链接的些许层(layer) 组成， 其中肇端层称为输入层(input layer)， 收受神经会聚的输入; 间隔层称为输出层(output layer)， 输出神经会聚的运行驱散， 其他中间的层称为掩盖层(hidden layer)， 它们是神经会聚运行的中间驱散. 每一个层由些许神经元(neuron) 组成， 每一个神经元对应一个浮点数变量. 一般的FNN从输出层运行读取输入， 并按相邻两层界说的函数逐层礼貌盘算推算， 直到得到输出. 因此， 在数学上神经会聚可以建模成一个多元函数 $ f: \mathbb R^m \to \mathbb R^n $ ， 且它可以线路成神经会聚中相邻层之间界说的函数的复合. 神经会聚层与层之间的函数大体可分为仿射函数和非线性函数两类， 仿射函数往往在FNN中的以全链接层、卷积层或平均值池化层等式样出现， 非线性函数主要包括非线性的激活函数， 如ReLU、Sigmoid、tanh等， 以及最大值池化层. 咱们最关心的是履行分类任务的神经会聚， 此时神经会聚的输出向量代表每一种分类的评分或概率， 一般咱们录取评分或概率最高的类为分类的驱散， 因此履行分类任务的神经会聚 $ f: \mathbb R^m \to \mathbb R^n $ 的分类输出可以线路为 $ C_f(x)= \arg\max_{1 \leqslant i \leqslant n} f(x)_i $ ， 其中 $ f(x)_i $ 代表实数向量 $ f(x) $ 第 $ i $ 个重量的值.
在先容神经会聚的鲁棒性之前， 咱们领先梳理神经会聚的安全性质. 安全性质(safety property) 是指在给定的要求下， 一个系统完陈规则的功能、不失效的才略， 直不雅上来看即为系统不会产生不安全的活动. 举例“智能汽车永远不会撞到行东说念主以偏激他粉饰物”就是一个安全性质. 由于这种广义上的安全性质很难被式样化地界说， 本文主要关心将安全性质甩掉到神经会聚中的研究， 即考证神经会聚 $ f $ 对于给定的输入聚集 $ X $ ， 其对应的输出范围 $ f(X) $ 是否齐在一个“安全”的聚集内. $ f(X) $ 称为神经会聚 $ f $ 对于输入 $ X $ 的可达集(reachable set)， 可达集分析相关的职责包括[45， 64]等. 咱们于界说1[23]式样化地界说神经会聚的安全性质.
界说1 (安全性). 给定神经会聚 $ f: \mathbb{R}^m\rightarrow \mathbb{R}^n $ ， 输入样本聚集 $ X\subseteq\mathbb{R}^m $ 以及安全范围 $ P\subseteq\mathbb{R}^n $ ， 如果神经会聚 $ f $ 对于 $ X $ 的可达集 $ f(X)\subseteq P $ ， 咱们称神经会聚 $ f $ 在输入 $ X $ 下振作性质 $ P $ ， 这个安全性质记为 $ (X， P) $ .
考证此类安全问题的算法在给定神经会聚 $ f $ ， 输入聚集 $ X $ 以及性质 $ P $ 之后， 会输出“Yes”“No”或者“Unknown”的考证驱散， 分别线路考证算法得出神经会聚 $ f $ 振作、烦恼作以及无法顺服是否振作安全性质 $ (X， P) $ 的论断. 如果一个安全性考证算法得出“Yes”论断时蕴含神经会聚 $ f $ 一定振作安全性质 $ (X， P) $ ， 咱们称该考证算法是可靠的(sound). 直不雅上来看， 可靠的算法判断神经会聚可达集 $ f(X) $ 的上近似(over approximation) 是否振作给定的性质 $ P $ . 反之， 如果考证算法不输出“Yes”的论断蕴含神经会聚 $ f $ 一定违背安全性质 $ (X， P) $ ， 咱们称该考证算法是完备的(complete). 完备的考证算法判断神经会聚可达集 $ f(X) $ 的下近似(under approximation)是否存在违背性质 $ P $ 的反例. 考证算法的可靠性和完备性之间的筹商可以参考图 1.
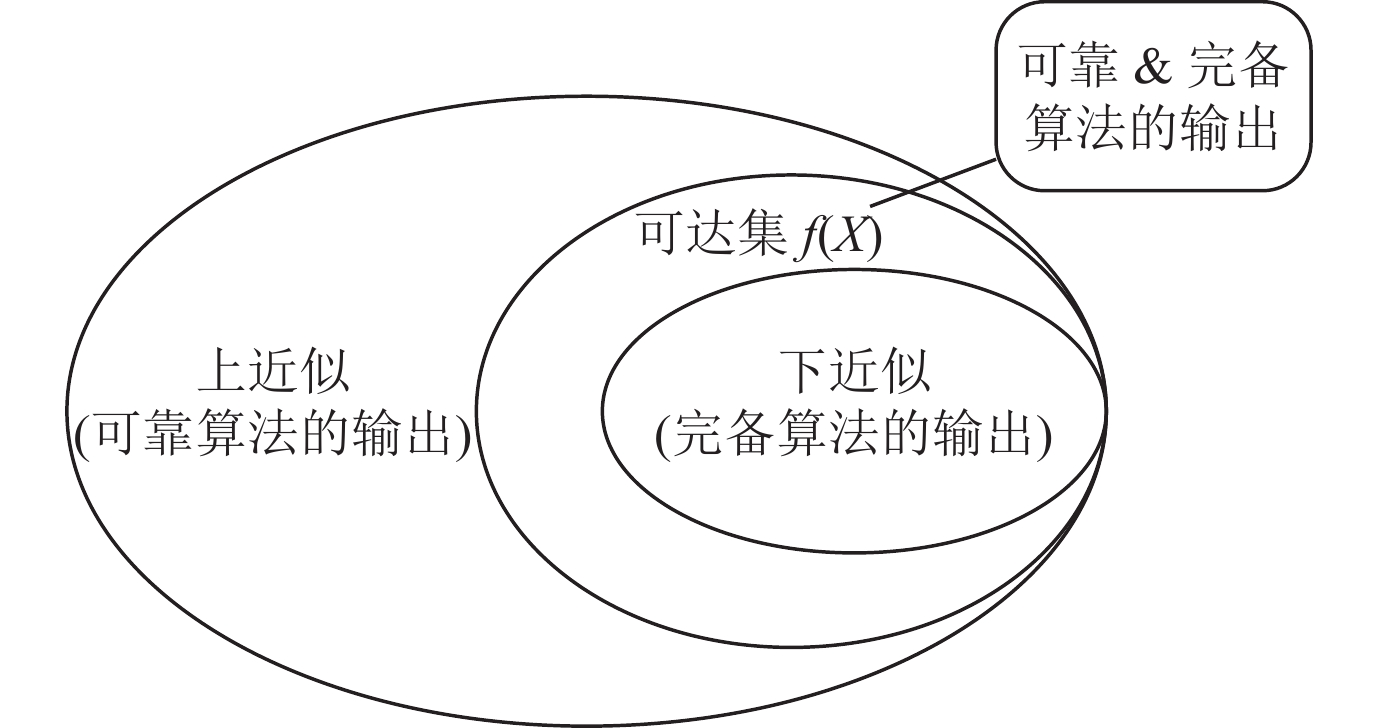图 1 可靠性和完备性线路图
在安全性的界说中， 将输入集 $ X $ 甩掉为单个样本 $ x_0\in\mathbb{R}^m $ 周围的一个扰动区域， 咱们一般用 $ l_p $ 范数下半径为 $ r $ 的球来线路， 记为 $ X= B_p(x_0， r)\subseteq\mathbb{R}^m $ ， 将安全范围 $ P $ 界说为聚集 $ P=\{y\in\mathbb{R}^n\mid \arg \max_i y_i=C_f(x_0)\} $ ， 安全性质 $ (X， P) $ 即称为局部鲁棒性(local robustness). 直不雅上看， 神经会聚的局部鲁棒性是指当输入的信息因为被袭击而产生一个有限范围内的小扰动时， 神经会聚仍然概略保捏正确的输入-输出关系的特色， 即对扰动后的输入仍然可以作念出正确的输出有计议. 神经会聚的局部鲁棒性可以式样化描摹如界说2.
界说2 (局部鲁棒性). 给定一个神经会聚 $ f $ 和输入样本 $ x_0 $ ， 以及样本 $ x_0 $ 周围半径为 $ r $ 的扰动区域 $ B_p(x_0， r) $ ， 如果性质:
$ \forall x\in B_p(x_0， r)， C_f(x)=C_f(x_0) $成立， 咱们称神经会聚 $ f $ 对于样本 $ x_0 $ 在扰动区域 $ B_p(x_0， r) $ 内具有局部鲁棒性.
在本文中， 咱们主要关心神经会聚的鲁棒性质， 如果莫得独特说明， 后文对于神经会聚安全性的考证方法均为局部鲁棒性的考证.
在当然语言处理和语音识别等领域， 应用最为以前的是RNN. 由于RNN比FNN的结构愈加复杂， 界说输入序列的扰动空间也愈加发愤， 因此对于RNN鲁棒性考证的职责目下还比较少， 且多数RNN的考证职责模仿了FNN的考证念念想. 本文将领先归来FNN鲁棒性考证的相关内容， 分析和比较FNN和RNN考证方法之间的里面筹商， 并就RNN考证濒临的挑战张开究诘.
3 FNN考证的研究近况目下针对FNN的考证方法主要分为两大类: 一类是基于可振作性模表面， 羼杂整数线性计议等优化表面的精准考证方法; 另一类主若是基于凸优化， 抽象解释等近似考证方法. 在后文图 2中， 咱们挑选出每一类中比较有代表性的考证方法进行对比[22-26，29-33，38-42，45-47，49-53，64-72]. 其中不同面目线路不同的考证方法类别， 箭头线路被指向的器具对箭头开拔的器具有升迁或者是由其模仿而来， 疏通面目的矩形方框中考证器具的精度疏通. 接下来将抽象先容具体的考证方法.
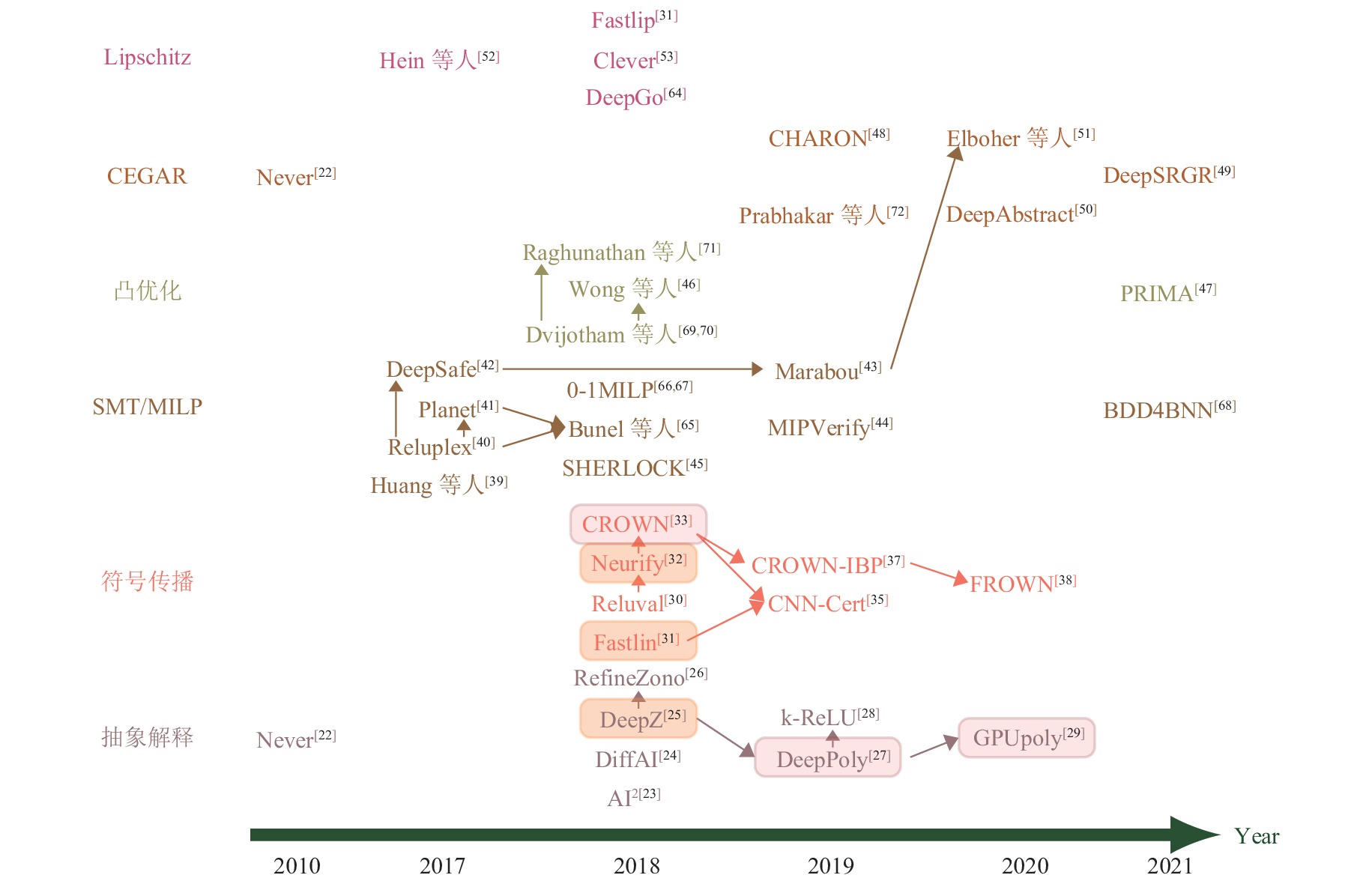图 2 主要的FNN考证方法对比
3.1 精准考证方法
由于神经会聚往往限制很大， 何况具有非凸的结构， 是以考证神经会聚的复杂度很高. 文件[40， 73]强调即使考证一个很浅显的性质亦然一个NP实足问题. 目下， FNN鲁棒性的精准考证方法主要包括基于可振作性模表面(satisfiability modulo theory， SMT) 以及羼杂整数线性计议(mixed integer linear programming， MILP) 这两大类. 基于SMT的考证方法将神经会聚鲁棒性考证问题编码为可振作性问题， 然后利用SMT求解器进行考证. 而基于MILP的考证方法是将神经会聚的仿射变换以及ReLU激活函数编码为MILP公式(常用的编码方法包括大M法[74]等)， 并精准地求解出FNN的可达集， 再判定该可达集是否振作给定的安全性质.
3.1.1 基于SMT的考证方法比较早期的考证方法包括Bastani等东说念主[75]的职责， 他们为神经会聚界说了两种不同的鲁棒性， 并利用线性管理来编码通盘神经会聚的鲁棒性考证问题， 从而将考证问题转动为可振作性问题. 他们通过将输入甩掉在ReLU函数只取赶巧或0的区域， 将蓝本的管理毒害为一个凸管理问题， 从而进行快速求解. Fawzi等东说念主[76]建议了一个表面框架来分析分类器抗扰动的鲁棒性， 并在表面上给出了鲁棒性的一般上界. Scheibler等东说念主[77]商量了倒立摆的模子锤真金不怕火问题， 倒立摆的限制器是一个具有非线性激活函数的神经会聚. 他们使用SMT求解器iSAT3进行求解， 实验标明对于只具有26个节点的神经会聚， 处置这个考证问题照旧颠倒具有挑战性. Narodytska等东说念主[78]建议二值化神经会聚(binarized neural network， BNN) 可以编码为布尔公式， 并利用SAT求解器对其进行鲁棒性考证， 这亦然初次给与精准的布尔编码来考证神经会聚的方法， 实验驱散露馅此考证方法可以处理限制为几百个神经元的神经会聚.
以上几种考证神经会聚的方法需要对会聚结构或性质作念出权贵的简化， 举例Bastani等东说念主[75]仅商量统共ReLU函数齐固定在激活或非激活状态的小输入区域， 只可考证所需性质的近似值. 基于SMT的考证方法需要求解大限制的管理问题， 因此这类将鲁棒性考证问题编码为SMT公式的考证方法在可拓展性上具有彰着的瓶颈.
Huang等东说念主[39]商量了外部要求变化(举例划痕和不同的天气要求等)对神经会聚分类器形成的影响. 比较于前边的职责， 他们基于SMT建议了一种愈加生动的鲁棒性考证方法， 对于一个特定的输入点 $ x $ ， 给与闹翻化的技艺将 $ x $ 邻域的无尽集简化为有限点集， 从而对扰动区域进行穷举并逐层传播. 实验标明这种闹翻化的考证技艺以致可以在VGG16等大型神经会聚上进行考证实验.
Katz等东说念主[40]建议了Reluplex， 将单纯形法(simplex algorithm) 加以拓展得到一个能处理ReLU激活函数的SMT求解器. 具体地， 他们将FNN的仿射变换编码为原子命题的合取式样， 将被ReLU激活的神经元 $ v $ 拆分红 $ v_b $ 和 $ v_f $ ， 分别链接前一层和后一层神经元. 他们将神经元分类为基变量和非基变量， 并为SMT求解过程界说了一系列更新司法， 直到求解算法间隔， 终末即可求出违背性质的反例， 或证明神经会聚的安全性.
Katz等东说念主在Reluplex职责中商量的鲁棒性考证问题为无东说念主机防碰撞系统ACAS Xu[79]中的些许安全性质， 每个ACAS Xu[79]会聚包含300个掩盖神经元. Reluplex仅撑捏ReLU激活函数， 何况这种完备的考证方法具有精准考证效力低下的问题. 因此， 这类基于SMT求解的考证方法无法胜利应用到现实中包含数十万个神经元的智能系统[80， 81]. Katz等东说念主[81]先容了对抗鲁棒性以偏激他种类的鲁棒性， 商量了考证工业界神经会聚濒临的问题， 并针对自动驾驶系统中FNN限制器的安全性问题， 建议了不时Reluplex进行考证的畴昔计议.
为了考证含有最大池化(maxpool)节点的神经会聚， Ehlers建议了一种基于SMT求解和线性计议的精准考证器具Planet[41]. 他们通过为ReLU激活函数和Maxpool函数添加线性贴近来线性地描写神经会聚的合座活动， 并通过添加冲突字句寻找不可行子集以减少搜索空间， 从而升迁搜索效力， 实验标明Planet可以考证具有上千个神经元的神经会聚.
Xiang等东说念主[82]通过可达集分析来考证多层感知机(multi-layer perceptron， MLP) 的安全问题， 这是一种结构浅显的神经会聚. 他们引入了“最大机灵度”的认识， 并通过求解凸优化问题来盘算推算具有单调激活函数的MLP的最大机灵度， 将神经会聚的可达集臆想问题转动为一系列优化问题并求解. 终末他们基于可达集臆想的驱散开发出一种可靠的自动考证算法.
Gopinath等东说念主建议了一种自动识别输入空间安全区域的完备考证方法DeepSafe[42]， 考证神经会聚的对抗鲁棒性. 该方法通过数据指引的聚类识别出“候选”安全区域， 然后证据这些区域的安全性， 或者提供证明它们不安全的反例. 他们在MNIST数据集和ACAS Xu会聚上评估发现DeepSafe可以准确地顺服神经会聚的安全输入区域.
Katz等东说念主在Reluplex[40]的基础之上又建议了Marabou[43]， 撑捏具有狂妄线性激活函数的FNN和卷积神经会聚(convolutional neural network， CNN)的考证， 在应用以前性上相对于前身Reluplex有了新的冲破. Marabou是基于SMT的考证框架， 其内置了基于单纯形法的线性计议求解器， 并诞生了一个很小的超时阈值， 当求解时候达到该阈值时， 求解器将考证过程诀别为更浅显的子过程， 在不同节点上并行地运行子查询. 比较于Reluplex在每次迭代中齐要将线性计议问题翻译成外部求解器GLPK承袭的输入， 并从中索取相应的驱散， Marabou大大升迁了线性计议问题的求解效力. 在ACAS Xu会聚上的实验标明， Marabou比较于Reluplex和Planet等器具在考证效力上具有彰着的上风.
Zhang等东说念主建议了BNN的分析框架BDD4BNN[68]. 他们将BNN视为黑盒， 将BNN和输入区域编码为可以线路为布尔函数的二进制有计议图(binary decision diagrams， BDD) 并基此想象了BNN的鲁棒性分析框架， 何况撑捏可解释性分析， 实验标明BDD4BNN框架可以考证上千个神经元的神经会聚.
基于SMT的考证方法由于编码过程时候代价腾贵， 在管理空间限制重大的情形下， 往往只可处理神经元数目在几千以内的神经会聚， 何况SMT求解器具有难以求解非线性问题的局限性， 基于SMT的鲁棒性考证方法往往只可处理ReLU或者其他具有线性激活函数的神经会聚.
3.1.2 基于MILP的考证方法神经会聚可以被编码为MILP公式. 在较为早期的研究中照旧有了相关的职责， 举例Fischetti等东说念主建议的0-1 MILP框架[66， 67]， 用一语气变量来线路每一个神经元的输出值， 闹翻变量线路ReLU激活过程; Lomuscio等东说念主[83]利用大M法将FNN编码为MILP公式， 何况将FNN的可达性问题编码为LP问题进行求解等.
Cheng等东说念主[84]开发了基于MILP的启发式算法， 并给与了一些优化方法升迁求解效力. 举例在用MILP求解神经元范围时， 同期商量前几层的神经元范围， 将全局MILP问题分割为些许个更小的子问题; 为不同掩盖层的神经元诞生编码优先级等. 以上优化方法权贵地减少了MILP求解器的运行时候， 与普通的MILP编码过程比较， 他们的优化政策在一些特殊的MNIST基准数据集上以致可以使得运行效力升迁两个数目级.
Dutta等东说念主建议了一种有用的可达集估盘算推算法SHERLOCK[45]， 在MILP全局优化和基于局部搜索的局部优化之间不休迭代， 通过修剪次优节点， 有用升迁了激活神经元的搜索速率. SHERLOCK很好地利用了神经会聚的局部一语气性和可微特色， 同期又幸免了局部搜索可能堕入局部最小值的窘境， 在效力上也优于传统的实足基于SMT或者MILP的考证方法. 实验露馅SHERLOCK能考证具有6000个神经元的神经会聚. 该算法专注于考证以ReLU动作激活函数的FNN， 而对于其他类型的激活函数， 举例Sigmoid和tanh， SHERLOCK不具备求解才略.
需要贯注的是， SHERLOCK固然利用了MILP技艺求解神经会聚的输出范围， 然而在编码ReLU函数的过程中添加了一个微弱的毒害， 因此SHERLOCK得到的是神经会聚输出的上近似. 为了便于归类， 咱们仍于此处先容SHERLOCK方法.
Bunel等东说念主[65]利用分支限界等优化方法， 将Reluplex、Planet等基于SMT、MILP的主流考证方法纳入一个斡旋的考证框架中， 并强调Reluplex、Planet在该框架中仅仅一个特例. 他们另一个进击孝顺在于从现存的神经会聚考证文件中采集并拓展得到一个新的基准数据集(benchmark) 并定名为PCAMNIST， 并在此数据集上将分支限界处理后的Reluplex和Planet等算法进行比较， 同期通过在更小的区域上精化ReLU的高低界， 采纳分支政策分割输入域等优化方法， 对以上考证算法建议了可能的改造， 大大提高了算法效力.
利用MILP考证神经会聚的比较有影响力的职责还包括Tjeng等东说念主建议的MIPVerify[44]， 他们将神经会聚编码为MILP问题并求解， 想象了一些剪枝方法减轻搜索空间， 大大提高了求解效力， 照旧可以考证中等限制的神经会聚， 相对于之前的基于SMT的考证方法驱散了不小的冲破， 以致可以拓展到带有卷积层和残差层的会聚结构中.
固然基于SMT和MILP的考证方法概略精准地顺服神经会聚的可达集， 何况连年来在神经会聚鲁棒性考证领域中取得了很大的进展， 然而由于此类方法具有编码复杂、时候代价大的舛错， 能考证的会聚限制比较小， 拓展到具有上万个神经元的神经会聚仍然具有很大的挑战. 同期， 在许多现实情况下， 考证神经会聚的性质并不需要得出其果然的可达集， 即如果可达集的上近似振作某安全性质， 则该可达集势必也振作这一性质. 因此从2018年掌握运行， 更高效的近似考证方法迟缓兴起.
韩国三级 3.2 近似考证方法FNN的近似考证方法比较于为数未几的可靠且完备的精准考证方法来说， 正处于快速发展的状态， 主要的近似考证方法包括基于抽象解释、标记传播、Lipschitz、凸优化以及反例指引的抽象-精化等考证方法.
3.2.1 基于抽象解释的考证方法基于抽象解释考证神经会聚的方法主若是利用抽象域在神经会聚中逐层传播， 终末得到神经会聚可达集的上近似， 并判断该上近似是否振作给定的安全性质. 最早的神经会聚考证方法是由Pulina等东说念主建议的Never[22]考证框架， 这亦然最早的利用抽象解释考证神经会聚的框架. 他们用区间界说神经会聚 $ f $ 的安全性， 即对狂妄给定的输入 $ x $ ， 分析输出 $ f(x)\in [l， u] $ 是否成立， 其中 $ l $ 和 $ u $ 线路给定的“安全阈值”. 他们将SMT求解器与反例指引的抽象-精化方法不时起来， 对MLP这种特殊的会聚结构进行安全性考证. 他们利用区间线路对每一层神经元的范围进行抽象， 并为非线性的Sigmoid激活函数添加些许个上近似的区间管理， 从而为神经会聚的每一层范围添加可靠的Box抽象域. 当传递到终末一层发现演叨反例时， 会触发神经会聚进行自动设立， 对激活函数进行更精致的诀别， 提高考证精度. 固然只得胜地考证了包含6个神经元的神经会聚， 但该方法初次将式样化考证和抽象解释的念念想应用到神经会聚考证中， 具有草创性的历史道理. 他们在随后的职责中[85， 86]比较了SMT求解器的性能对MLP考证效力的影响， 并分析发现固然现时最先进的SMT求解器有才略处置MLP考证领域中的一些进击问题， 然而对践诺限制和细粒度抽象会聚的考证， 仍然是一个经久的绽放性挑战.
为了将抽象解释的考证方法拓展到限制更大， 结构更一般的神经会聚中， Gehr等东说念主建议了第1个可靠、可拓展的ReLU神经会聚考证框架AI2[23]. 他们利用区间抽象域和Zonotope抽象域[87]为扰动之后的输入添加一个可靠的范围， 并构造了基于Zonotope的抽象调理器来履行神经会聚中的各式非线性操作， 包括ReLU激活函数和最大池化层， 终末考证输出的Zonotope是否振作给定的性质. 由于Zonotope骨子描画浅显， 对真实可行域的毒害在有些考证场景中过于宽松， 何况在传播过程中会逐层放大邪恶， 其考证精度有所局限.
Mirman等东说念主建议了一种基于羼杂Zonotope的鲁棒性教师和考证方法DiffAI[24]. 羼杂Zonotope是指在Box抽象域的基础之上添加一些形如Zonotope的偏移量， 动作一个抒发才略等同于Zonotope的新抽象域. 他们在此基础上界说了一个耗损函数来教师神经会聚， 并通过梯度下落等技艺进行优化， 通过这种方法教师得到的会聚具有精采的鲁棒性和可拓展性. Mirman等东说念主在后续的职责[88]中引入了两个新认识: ① 用于微调抽象精度和可彭胀性的抽象层; ② 用一种生动的领域专用语言(domain specific language， DSL) 来描摹神经会聚中抽象耗损与具体耗损相不时的办法函数， 并建议为大型残差会聚ResNet提高鲁棒性的教师方法.
Singh等东说念主建议的DeepZ框架[25]进一步处置了AI2的可拓展性问题， 适用于ReLU， Sigmoid， tanh等多种激活函数和前馈、卷积以及残差会聚等多种神经会聚结构. 访佛于AI2， DeepZ也给与了Zonotope抽象域对神经会聚的扰动区域进行毒害， 但DeepZ利用面积最小化道理为ReLU， Sigmoid， tanh等激活函数提供了一种更紧的可靠的抽象阵势， 并利用Zonotope在神经会聚中的传播求解终末一层神经元的范围， 从而考证会聚的鲁棒性.
以上考证方法齐是利用Zonotope抽象域在神经会聚中逐层传播， 是现时神经会聚鲁棒性考证领域比较主流的方法. 然而这种不完备的毒害方法会导致在每一个神经元履行激活操作时引入比较大的邪恶， 何况在传播过程中也会形成精度耗损. 因此该抽象域在毒害精度上存在劣势， 终末一层神经元的范围可能会被放大成百上千倍.
Singh等东说念主建议了DeepPoly[27]， 进一步升迁了抽象域的精度. DeepPoly基于线性不等式， 为每个神经元添加两个标记界管理 $ a_i^\leqslant $ ， $ a_i^\geqslant $ 和两个数值界管理 $ l_i $ ， $ u_i $ 动作抽象域， 并建议了两种三角形毒害方法， 为ReLU激活函数添加一组毒害范围， DeepPoly通过反向传播每一个神经元的标记界到输入层， 再代入输入层神经元的范围求解出神经元的数值界. 相较于前边几种考证方法， DeepPoly在考证效力和精度上齐具有彰着的上风.
为了处置Zonotope抽象域带来的精度耗损问题， 许多新的考证方法也在此基础上应时而生. Singh等东说念主建议了RefineZono[26]， 将Zonotope抽象域和MILP、LP不时起来考证神经会聚. 他们用Zonotope抽象域求解得到每一层神经元的范围， 然后利用MILP求解器精化该范围， 从而得到更紧的神经元范围， 再进一步往前传递分析. RefineZono得到了比DeepPoly更高的考证精度， 然而MILP的应用导致运行时候上存在一些劣势.
为了更进一步地升迁传递效力， Müller等东说念主将区间分析的高效传播和DeepPoly的高精度这两个上风不时起来， 并利用了GPU的并行性建议了GPUPoly框架[29]来考证神经会聚. 在DeepPoly框架中， 得到神经元的数值高低界需要反向传播到输入层， 因而效力低下， GPUPoly利用区间分析来代替这一反向传播过程: 在求解每个神经元的数值界时， 他们为神经元的范围添加一个可靠的区间抽象， 如果现时神经元处于顺服的激活或者未激活状态， 即可不祥反向传播的过程， 反之则利用DeepPoly反向传播得到神经元的高低界. 收获于高并行的想象， GPUPoly的精度等同于DeepPoly， 然而考证速率比DeepPoly快35倍到170倍.
此外， Singh等东说念主还在DeepPoly的基础上建议一种带参数的精化框架k-ReLU[28]， 在求解每一层神经元的标记界时， 同期商量 $ k $ 个神经元的管理， 并为其添加一个统共为0或± 1的八面体(octagon)管理. k-ReLU玄妙地处置了DeepPoly在求解神经元管理时只可商量单个神经元， 而忽略了神经元之间的相互筹商的问题. 在实验中也体现出k-ReLU的考证精度比较于DeepPoly有彰着的升迁. 但由于k-ReLU框架中新增的管理个数是 ${\rm{O}}(2^k)$ ， 时候复杂度随 $ k $ 呈指数的速率增长， 因此 $ k $ 的取值往往较小， 一般取为2或3， 最大可达到7.
上述基于抽象解释的考证方法以较高的效力得到神经会聚一个可靠的输出范围， 何况可以拓展到中等限制的神经会聚. 由于神经会聚真实的可达集真包含于抽象解释得到的输出范围， 当抽象域过于毒害的时候， 很容易产生演叨反例. 即， 若抽象解释得到的范围烦恼作给定的性质， 便很难证考证真实的输出是否振作该性质， 这亦然考证算法可能会得到“Unknown”驱散的原因. 因此产生了反例指引的抽象-精化框架来考证神经会聚.
3.2.2 基于会聚结构抽象/反例指引的抽象-精化的考证方法当考证算法对神经会聚的抽象过于毒害时， 输出范围中可能含有许多不属于安全范围内的“反例”. 如果这些“反例”对应的原始输入经过神经会聚传递之后得到的真实输出是属于安全范围的， 咱们将这些“反例”称为“假反例”; 反之， 若这些“反例”的原始输入对应的输出也在安全范围以外， 则称为“真反例”， 其直不雅含义如图 3所示. 基于反例指引的抽象-精化方法(counterexample guided abstraction refinement， CEGAR) 通过抽象模子得到的假反例， 将过于毒害的抽象进行精化， 从而迭代地得到一个更精准的考证驱散.
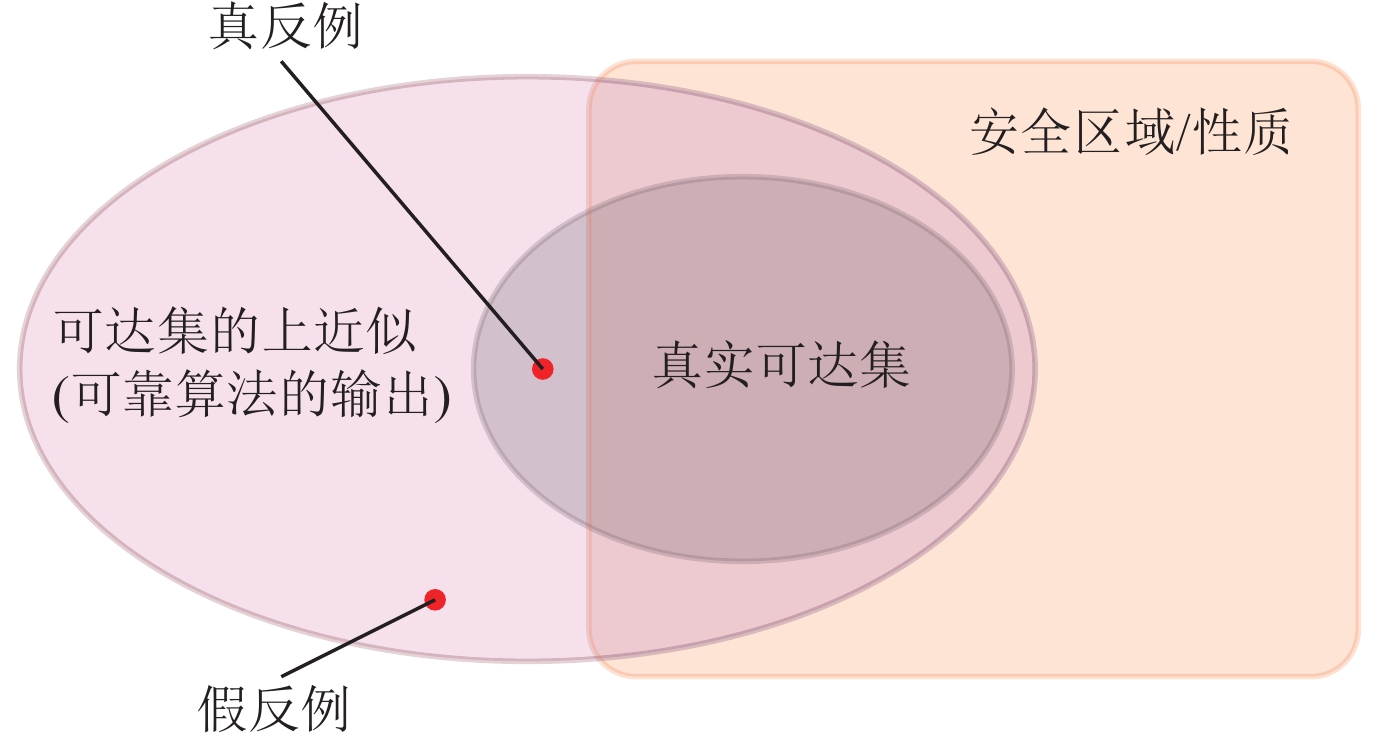图 3 真反例和假反例线路图
反例指引的抽象-精化方法往往会与抽象解释等毒害方法不时起来考证神经会聚的鲁棒性. 其道理为: 利用抽象解释考证神经会聚时， 如果因为对可达集毒害过大而无法考证给定的安全性质， 就会触发精化方法得到更紧的抽象域或者更细粒度的抽象. 举例前边先容的Never框架[22]， 当利用抽象解释在可达集的上近似中发现反例时， 会触发神经会聚的自动设立， 这是比较早期的将抽象与精化不时起来考证神经会聚的方法.
除了与抽象解释相不时， 精化方法还可以与其他的毒害阵势相不时考证会聚， 举例对会聚结构进行抽象. 对会聚结构进行抽象的方法主要通过删除、合并过剩的神经元来减小神经会聚的限制， 并得到神经会聚输出范围的上近似. 关联词改造神经会聚的结构很可能因为过度放大权重导致输出范围过度毒害， 此时基于反例指引的抽象-精化方法可以得到更紧、更准确的输出范围.
早在2015年， Srinivas等东说念主[89]建议可以通过移除神经元简化神经会聚的结构， 同期保捏和原始神经会聚不异的性能. 他们盘算推算传入某一层神经元的权重之间的不异性度量， 然后通过合并那些最不异的权重来移除“过剩”的神经元， 并对移除神经元的数目和准确性之间的关系进行了分析. 访佛地， Zhong等东说念主[90]通过聚类对权重进行合并， 从而压缩神经会聚的限制. Han等东说念主[91]引入了“深度压缩”方法——一个3阶段的职责经由: 修剪、量化权重和霍夫曼编码， 在不影响神经会聚准确性的要求下压缩神经会聚的限制， 使得神经会聚的存储需求减少数十倍. 以上通过修剪、抽象会聚结构来压缩神经会聚的方法， 目的是减少神经会聚的内存蹧跶， 并分歧神经会聚的安全性进行考证.
对于利用抽象会聚结构来考证神经会聚的安全性的职责， Prabhakar等东说念主[72]商量了FNN的可达性分析问题. 他们将神经会聚的权重矩阵和偏差向量分别抽象为区间， 形成区间神经会聚(interval neural network， INN)， 线路图如图 4所示. 具体地， 他们将团结掩盖层的两个神经元合并到沿路， 与这两个神经元筹商的权重和偏差将拓展为区间的式样， 该区间是合并之前神经元权重和偏差的凸包， 从而确保合并后会聚的输出为原神经会聚可达集的上近似. 他们利用MILP编码最终得到的区间神经会聚并求解输出范围. 通过这种方法将神经会聚抽象为一个结构更浅显、神经元数目更少的区间神经会聚， 驱散盘算推算复杂度和输出精度之间的量度. 由于被合并神经元的录取对最终的精度影响很大， 因此如何通过采用合适的神经元提高抽象神经会聚的精度， 以及当神经会聚过于毒害时如何采纳精化次第来修正抽象过程是这项职责的难点.
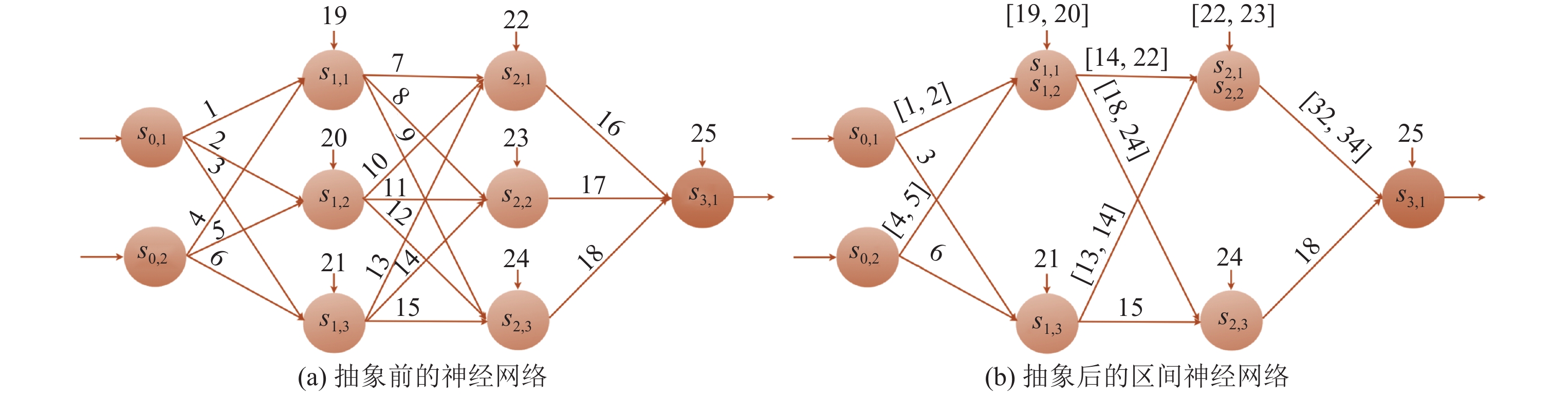图 4 通过将普通FNN的权重矩阵元素抽象为区间线路可以减少神经元数目， 神经元上方的数字线路偏差
可靠的Zonotope抽象域可以顺服神经会聚输出范围的上近似， 然而由于抽象域过于毒害， 会往往导致假反例的产生. 另一方面， 基于优化寻找反例的过程可以高效地寻找到对抗性扰动， 但如果莫得搜索到反例， 则很难证明神经会聚是鲁棒的. Anderson等东说念主将这两种政策的上风相不时， 建议了鲁棒性考证方法CHARON[48]， 在考证的同期寻找反例， 又利用找到的反例对抽象过程进行精化. 这是一种可靠且 $ \delta $ -完备的考证方法. 其中 $ \delta $ -完备是指如果一个性质 $ P $ 被反例 $ x_* $ 证伪， 则 $ x_* $ 的 $ \delta $ 邻域内势必存在委果的反例. 另外他们还建议了自动学习考证政策的方法， 可以为反例搜索提供带领.
Ashok等东说念主建议一个适用于全链接FNN的抽象框架DeepAbstract[50]， DeepAbstract基于启发式的K-means聚类方法， 将在输入上表现不异(I/O不异)的神经元进行聚类， 然后在团结层中合并这些具有I/O不异性的神经元， 从而减小神经元的限制， 提高考证效力. 与纯正的压缩技艺比较， 他们的抽象提供了原始神经元和抽象神经元之间的一个映射， 便于将抽象会聚的鲁棒性考证驱散革新到原始神经会聚上， 从而得到原始神经会聚的考证驱散. 在实验中他们展示了如何利用DeepPoly考证抽象会聚， 并迁徙到对原始神经会聚的考证中.
Elboher等东说念主[51]通过对神经元的性质进行分类， 将每个神经元分为pos/neg和inc/dec这4种类型， 并迭代地将类别疏通的神经元进行合并， 减小神经会聚限制. 他们利用Marabou来考证抽象之后的会聚， 并在抽象过于毒害的情况下给与反例指引的抽象-精化， 对神经会聚结构的抽象进行细化. 这类方法将抽象带来的高效力与反例指引的抽象-精化带来的高精度相不时， 很好地驱散了神经会聚考证精度和效力上的均衡.
在最近的职责中， Yang等东说念主在DeepPoly抽象域的基础上， 建议了伪区域带领的神经会聚考证精化技艺DeepSRGR [49]， 该方法在考证精度需求较高， DeepPoly抽象域难以得胜考证的风光， 可以利用通过性质取反构造的伪区域， 精化枢纽变量在伪区域语义中的高低界， 从而大幅升迁DeepPoly抽象域的考证精度. 在该方法的框架下， 每次精化的过程并不会生成具体的反例， 用于带领精化的是伪区域的管理和伪区域语义核心纽变量更好的界.
基于反例指引的抽象-精化方法还可用于教师和考证深度强化学习(deep reinforcement learning， DRL) 系统. Jin等东说念主建议的TRAINIFY框架[92]可以在抽象的状态空间下教师出一个DRL系统， 当教师得到的DRL系统产生某种安全性质的反例时， TRAINIFY凭证该反例优化抽象状态空间， 并在更精致的抽象状态上再次教师DRL系统. 通过重叠以上过程就可以教师出一个精度高、鲁棒性好的DRL系统.
上述基于会聚结构抽象和反例指引的抽象-精化方法通过将表现不异的神经元进行合并或删除， 减小会聚限制， 然后利用现存的方法(SMT、MILP等)来考证神经会聚的性质， 达到提高考证效力的目的， 终末得到的输出为神经会聚可达集的上近似. 当对神经会聚的结构抽象过于概略时， 此类方法会不时反例对抽象进行精化， 提高考证精度. 然而如何设定抽象神经元的模范以及如何达到精度与效力的均衡是此类方法的难点， 何况在抽象会聚结构的过程中需要对神经会聚再行编码， 时候代价比较高.
3.2.3 基于标记传播的考证方法基于标记传播的考证方法主要通过区间线路、线性毒害等阵势， 将神经会聚每一层之间的迁徙关系线路为一系列标记管理并逐层传递， 终末得到输出层与输入层之间的管理关系， 再将输入层的数值范围代入标记管理关系中， 得到输出范围. 由于对ReLU等激活函数采纳了线性毒害， 往往情况下， 此类基于标记传播的方法得到的输出范围亦然神经会聚可达集的上近似.
Gowal等东说念主[34， 93]建议了由区间盘算推算繁衍而来的区间范围传播(interval bound propagation， IBP)， 他们展示了如何利用IBP来教师可证明鲁棒性的大型神经会聚， 这是一种可以用于教师分类器的不完备算法， 其主要念念想是为神经会聚中每一层神经元的多面体管理添加一个轴平行的上近似范围框(本质上访佛于Box管理)， 该范围框老是包含真实的多面体管理. 此方法比较于Wong等东说念主[94]建议的基于对抗性教师的考证方法在扰动半径增大时有彰着的竞争力.
Weng等东说念主建议了一种与DeepZ访佛的考证框架Fastlin[31]， 可以求解 $ l_p $ 扰动下神经会聚可达集的上近似. Fastlin的核心念念想是利用仿射变换和平行四边形毒害导出输出层神经元的标记高低界， 逐层反向传播到输入层并代入输入层神经元的范围， 即可得到输出层神经元的范围. 由于Fastlin和DeepZ对于非顺服神经元的ReLU激活齐给与了疏通的Zonotope毒害， 如果神经会聚的非线性单位仅包含ReLU， 输入是 $ l_{\infty} $ 范数下的一个扰动邻域， 那么由Fastlin和DeepZ得到的输出范围是疏通的， 即这两种方法在 $ l_{\infty} $ 范数下的精度是等价的， 具体的证明如引理1. 而DeepZ给与的Zonotope抽象域传播比较于Fastlin给与的带线性管理的反向传播效力会更高， 因此实验驱散露馅DeepZ比Fastlin的效力高2.5倍以上.
引理1 (Fastlin和DeepZ的等价性). 激活函数为ReLU的神经会聚 $ f $ 的输入为 $ l_{\infty} $ 范数下的Zonotope时， 用Fastlin和DeepZ得到的输出范围是等价的.
证明: 设神经会聚 $ f $ 的权重矩阵和偏差向量分别为 $ \{W_i\in\mathbb{R}^{l_{i+1}\times l_{i}}\mid i=1， \ldots， n\} $ 和 $ \{b_i\in\mathbb{R}^{l_{i+1}}\mid i =1， \ldots， n\} $ ， 激活函数为 $ \{\sigma_i\in\mathbb{R}^{l_{i+1}}\mid i =1， \ldots， n\} $ ， 以及该激活函数在Fastlin和DeepZ框架下的毒害为 $ \{\sigma_i'\in\mathbb{R}^{l_{i+1}}\mid i =1， \ldots， n\} $ ， 输入范围为 $ X_1 = B_{\infty}(x， r)\subseteq\mathbb{R}^{l_1} $ ， 咱们用 $\{ X_i\subseteq \mathbb{R}^{l_i}\mid i=1， \ldots， n+1 \}$ 线路输入 $ X_1 $ 传递到每一层神经元之后得到的像. 则神经会聚在Fastlin和DeepZ框架下的输出范围即:
$ f(X_1) = W_n\cdot \sigma'_{n-1}(W_{n-1}\cdot\sigma'_{n-2}(\ldots \sigma'_1(W_1\cdot X_1+b_1)\ldots)+b_{n-1})+b_n， $其中， ·线路矩阵乘法， 对于Fastlin框架， 咱们以求解输出层第 $ i $ 个神经元 $ X_{n+1}^{(i)} = f(X_1)^{(i)} $ 的最大值为例， 若权重矩阵 $ W_n $ 的第 $ i， j $ 元 $ W_{n}^{(ij)} > 0 $ ， 第 $ n $ 层的像 $ X_{n} $ 的第 $ j $ 个元素 $ X_{n}^{(j)} $ 应代入激活函数 $ \sigma'_{n-1} $ 平行四边形毒害的线性上界， 反之则代入平行四边形毒害的线性下界. 由此逐层反向传播， 直到代入第1层神经元的范围 $ X_1 $ . 此过程等价于由第1层神经元的扰动范围 $ X_1 $ 从前去后传递， 对激活函数给与疏通的平行四边形毒害阵势， 逐层盘算推算得到终末一层神经元的范围. 因此咱们证明底下两种情形.
(1) 疏通的Zonotope经过仿射变换之后， DeepZ和Fastlin的输出是等价的Zonotope.
(2) 疏通的输入范围经过ReLU激活之后， DeepZ和Fastlin的输出范围疏通. 贯注， Fastlin只适用于ReLU激活函数的神经会聚.
对于情形1， 由于神经会聚在传播过程中轮流进行仿射变换和ReLU激活， 为了简化盘算推算， 咱们先忽略线路层数的下标. 设第1层仿射变换的输入为 $ X=\{x|a^- \leqslant x \leqslant a^+\} $ ， 则DeepZ中对应的Zonotope式样线路为 $ X= \{x|x = \dfrac{a^++a^-}{2} + \dfrac{a^+-a^-}{2}\cdot\epsilon， \epsilon\in[-1， 1]\} $ .
对于Fastlin输入范围中的任极少 $ x_0\in X $ ， 齐能独一找到DeepZ输入范围中 $ \epsilon_0 =\dfrac{2x_0-(a^++a^-)}{a^+-a^-} \in[-1， 1] $ 对应的点 $ x'_0 $ ， 使得经过仿射变换之后， $ Wx_0+b=W\left(\dfrac{a^++a^-}{2}+\dfrac{a^+-a^-}{2}\cdot \epsilon_0\right) + b=Wx_0'+b $ . 因此当Fastlin和DeepZ的输入范围是疏通的Zonotope时， 经过仿射变换之后得到Fastlin求解的范围包含于DeepZ得到的Zonotope范围. 反之， 对于DeepZ输入的Zonotope中狂妄 $ \epsilon_1\in[-1， 1] $ 对应的 $ x_1 $ ， 齐能在Fastlin输入中范围中找到对应的 $ x_1'= \dfrac{a^++a^-}{2}+ \dfrac{a^+-a^-}{2}\cdot \epsilon_1\in [a^-， a^+] $ ， 使得 $ Wx_1+b=W\left(\dfrac{a^++a^-}{2}+\dfrac{a^+-a^-}{2}\cdot \epsilon_1\right) + b=Wx_1'+b $ . 因此当Fastlin和DeepZ的输入范围为疏通的Zonotope时， 经过仿射变换之后得到DeepZ求解的范围包含于的Fastlin得到的范围， 从而Fastlin和DeepZ在仿射变换的过程是等价的(该情形也可以利用矩阵乘法张开来证明).
底下证明情形2. 情形1的证明可得出对于每个神经元经过Fastlin和DeepZ的仿射层传播之后会得到疏通的高低界 $ l $ 和 $ u $ . 底下咱们证明经过ReLU激活后DeepZ和Fastlin也得到疏通的范围. 若 $ l\geqslant0 $ 或 $ u\leqslant0 $ ， 则Fastlin和DeepZ框架激活之后均得到顺服的疏通的值， 对于激活程度不顺服的神经元( $ l\leqslant0 $ 且 $ u\geqslant0 $ )， Fastlin给与线性管理的阵势为其添加平行四边形毒害. 对于激活前的神经元 $ x\in [l， u] $ ， Fastlin求得的 $ ReLU(x) $ 的范围为: $ \dfrac{u}{u-l}\cdot x\leqslant ReLU(x)\leqslant\dfrac{u}{u-l}(x-l) $ . 而DeepZ得到的Zonotope毒害的中心为 $ \left(\dfrac{l+u}{2}， \dfrac{u^2}{2(u-l)}\right) $ ， 因此DeepZ得到的ReLU激活后Zonotope线路为: $ ReLU(x)=\left(\dfrac{l+u}{2}， \dfrac{u^2}{2(u-l)}\right)+\left(\dfrac{u-l}{2}， \dfrac{u}{2}\right)\cdot\epsilon_1 +\left (0， \dfrac{-ul}{2(u-l)}\right)\cdot\epsilon_2. $ 底下咱们证明二者求得的ReLU激活范围 $ \dfrac{u}{u-l}\cdot x\leqslant ReLU(x)\leqslant\dfrac{u}{u-l}(x-l) $ 和 $ ReLU(x)=\left(\dfrac{l+u}{2}， \dfrac{u^2}{2(u-l)}\right)+\left(\dfrac{u-l}{2}， \dfrac{u}{2}\right)\cdot\epsilon_1 + \left(0， \dfrac{-ul}{2(u-l)}\right)\cdot\epsilon_2 $ 是等价的.
对于狂妄 $ x\in [l， u] $ ， 咱们领先证明在Fastlin中经过激活后得到的范围 $ ReLU(x)\in\left[\dfrac{u}{u-l}\cdot x， \dfrac{u}{u-l}(x-l)\right] $ 包含于DeepZ得到的Zonotope中. 当 $ x = \dfrac{l+u}{2}+\dfrac{u-l}{2}\cdot\epsilon_1 $ 时， $ \dfrac{u^2}{2(u-l)}+\dfrac{u}{2}\cdot\epsilon_1+\dfrac{-ul}{2(u-l)}\cdot\epsilon_2=\dfrac{2ux-ul(1+\epsilon_2)}{2(u-l)} $ ， 由于 $ \epsilon_2\in[-1， 1] $ ， 是以上式的范围为: $ \dfrac{ux}{u-l}\leqslant\dfrac{2ux-ul(1+\epsilon_2)}{2(u-l)}\leqslant\dfrac{u(x-l)}{u-l} $ ， 昭着Fastlin在 $ x $ 处激活后的范围包含于DeepZ激活后的范围. 反之咱们证明对于狂妄的 $ \epsilon_1， \epsilon_2\in[-1， 1] $ ， DeepZ对应的激活后的 $ ReLU(x)=\dfrac{u^2}{2(u-l)}+\dfrac{u}{2}\cdot\epsilon_1+\dfrac{-ul}{2(u-l)}\cdot\epsilon_2 $ 也齐包含于Fastlin范围中. 对 $ \epsilon_1， \epsilon_2\in[-1， 1] $ ， $ x=\dfrac{l+u}{2}+\dfrac{u-l}{2}\cdot\epsilon_1 $ ， Fastlin得到的激活后的范围是 $ \dfrac{u}{u-l}\cdot\left(\dfrac{l+u}{2}+\dfrac{u-l}{2}\cdot\epsilon_1\right)\leqslant ReLU(x)\leqslant\dfrac{u}{u-l}\cdot\left(\dfrac{l+u}{2}+\dfrac{u-l}{2}\cdot\epsilon_1-l\right) $ ， 即 $ \dfrac{u(l+u)}{2(u-l)}+\dfrac{u}{2}\cdot\epsilon_1\leqslant ReLU(x)\leqslant\dfrac{u}{2}\cdot(\epsilon_1+1) $ . 由于 $ \dfrac{u^2}{2(u-l)}+\dfrac{u}{2}\cdot\epsilon_1+\dfrac{-ul}{2(u-l)}\cdot\epsilon_2- \dfrac{u}{2}\cdot(\epsilon_1+1)= \dfrac{ul(1-\epsilon_2)}{2(u-l)}\leqslant0 $ ， 且 $ \dfrac{u^2}{2(u-l)}+\dfrac{u}{2}\cdot\epsilon_1+\dfrac{-ul}{2(u-l)}\cdot\epsilon_2-\left(\dfrac{u(l+u)}{2(u-l)}+\dfrac{u}{2}\cdot\epsilon_1\right)=\dfrac{-ul(\epsilon_2+1)}{2(u-l)}\geqslant 0 $ ， 因此DeepZ求得的毒害范围包含于Fastlin求得的范围， 从而二者在ReLU激活函数的毒害上得到的范围亦然等价的.
要而论之， 可由归纳法证明出对于狂妄ReLU激活的神经会聚， 如果神经会聚的输入范围是Zonotope， 则经过Fastlin和DeepZ求出的输出范围是等价的.
Wang等东说念主建议了Reluval[30]， 这是一种基于标记区间传播的考证方法. Reluval为每一个神经元添加标记区间界， 访佛于DeepPoly的标记界. 对于ReLU激活函数的模拟， 他们给与区间分割的阵势， 将其中一部分心经元范围分割为些许个子区间的并集. 对于每个子区间， 该神经元很可能变成顺服的激活或不激活的神经元， 从而得到更精准的输出范围. 比较于Reluplex等精准考证方法的高复杂度和难拓展性， 以及Wong等东说念主[46]， Dvijotham等东说念主[70]建议的基于多面体毒害或凸优化带来的过度毒害问题， Reluval的区间盘算推算能相对高效地传播， 同期他们通过切割输入区间尽可能幸免过度毒害导致的假反例表象.
在接下来的职责中， Wang等东说念主[32]在区间分析和线性毒害分析[30， 41]的基础之上改造了Reluval框架， 得到精度和效力齐更高的考证器具Neurify. 比较于Reluval， 当神经元之间的依赖关系变得太复杂而无法进一步用标记线路时， Neurify通过添加一定的毒害来不时盘算推算神经元的范围， 和DeepZ、Fastlin这两种考证框架有不谋而合之妙. 事实上， Neurify、DeepZ以及Fastlin在考证精度上是等价的， 而比较于Reluval和Reluplex， Neurify在效力和精度上齐有彰着的上风.
以上考证方法会濒临如何将ReLU激活函数的毒害扩充到tanh和Sigmoid等其他激活函数的问题， Zhang等东说念主建议了通用的CROWN框架[33]， 通过一种自得当的毒害阵势为不同的激活函数添加标记线性范围来处置可拓展性问题. CROWN可以拓展到多种激活函数的神经会聚上， 以致可以给与二次函数为激活函数添加合适的毒害. 而对于ReLU神经会聚来说， CROWN践诺上和DeepPoly的精度是等价的. 比较于之前的方法， CROWN可以有用地考证限制超越一万个神经元、具有不同激活函数的神经会聚. 随后Salman等东说念主[95]建议了一个斡旋的分层凸毒害框架， 系统地讲述了DeepZ， Fastlin， Neurify， DeepPoly， CROWN等考证框架的关系， 从凸毒害和拉格朗日对偶这两个方面究诘了这些方法的考证效力， 并揭示了这类毒害方法在考证精度上具有的表面上限.
Li等东说念主[36]和Yang等东说念主[96]在标记区间算术的基础上， 进一步将标记传播和抽象解释不时， 将标记传播扩充到更一般的数值抽象域上， 驱散了器具DeepSymbol 和以此器具为基础的神经会聚考证平台PRODeep[97]. 值得一提的是， PRODeep是国内首个神经会聚考证平台， 它集成了管理求解、抽象解释和标记传播3类技艺， 并对它们进行了深度的不时.
前述大多数职责重心关心结构浅显的FNN的鲁棒性考证. Boopathy等东说念主[35]建议了一个通用且高效的CNN-Cert框架， 将深度神经会聚的鲁棒性考证拓展到了CNN， 可以处理包括卷积层、最大池化层、残差块等在内的多种神经会聚结构， 并撑捏多种激活函数. CNN-Cert框架通过利用卷积层的特殊结构， 使得Fastlin和CROWN仅仅其特例， 何况在鲁棒范围不异以致更好的情况下， 将二者的效力分别升迁了17倍和11倍.
基于IBP的考证方法在许多种情况下的效力彰着优于基于线性毒害的方法， 但IBP盘算推算得到的范围要比线性毒害宽松得多. 因此Zhang等东说念主建议了一种新的神经会聚对抗教师方法， 通过将前向传播中的IBP范围和反向传播中基于线性毒害的CROWN范围相不时得到CROWN-IBP[37]. 他们构造出一个对于IBP范围和CROWN-IBP范围的耗损函数， 通过最小化该耗损函数求解出神经会聚的参数， 使得教师之后的神经会聚不仅具有精采的分类精度， 还具有较高的鲁棒性. 在教师可考证的鲁棒神经会聚方面， CROWN-IBP具有很高的盘算推算效力， 何况得到的范围永久优于胜利利用IBP得到的范围， 很好地驱散了精度和效力之间的均衡.
Lyu等东说念主[38]在CROWN的基础上又建议了Fastened CROWN (FROWN)框架， 这是一种用于提高神经会聚鲁棒性的教师方法. 他们证明如果将神经元的高低界管理个数分别只甩掉为一个， 则比较于线性计议， CROWN得到的神经元的高低界是最优的. 他们在此基础上建议的FROWN可以进一步地缩紧CROWN提供的范围， 何况在表面上能拓展到其他类型神经会聚的考证方法中， 举例考证CNN的CNN-Cert以及考证RNN的POPQORN.
基于标记传播的考证方法将标记盘算推算的高效、可拓展性等上风应用到神经会聚考证中， 并取得了许多后果， 然而跟着神经会聚层数加多限制增大， 这类方法的抒发式也会变得愈加复杂， 何况在传递过程中会逐层放大邪恶.
3.2.4 基于Lipschitz的考证方法Szegedy等东说念主[98]证明带有ReLU激活函数或者最大池化层等结构的FNN和CNN是Lipschitz一语气的， 是以神经会聚的输出在高低界范围内的统共值齐是可达的. 因此一个比较当然的想法是从神经会聚自己的性质开拔， 利用Lipschitz常数来考证筹商性质. 咱们称一个神经会聚具有Lipschitz一语气性， 如果这个神经会聚振作界说3[61].
界说3 (Lipschitz一语气性). 给定两个度量空间 $ (X， d_X) $ 和 $ (Y， d_Y) $ ， 其中 $ d_X $ 和 $ d_Y $ 分别是聚集 $ X $ 和 $ Y $ 上的度量， 一个函数 $ f: X\rightarrow Y $ 是Lipschitz一语气的， 如果存在一个实数 $ K \geqslant 0 $ 使得对狂妄的 $ x_1， x_2 \in X $ ， 下列不等式齐成立:
$ \begin{array}{*{20}{l}} d_Y(f(x_1)， f(x_2))\leqslant Kd_X(x_1， x_2) \end{array} $ (1)其中， $ K $ 称为对于函数 $ f $ 的Lipschitz常数， 振作该不等式的最小的 $ K $ 值称为最优的Lipschitz常数， 往往用标记 $K_{{\rm{best}}}$ 线路.
对于Lipschitz考证方法， 比较早期的职责是Hull等东说念主建议的[99]. 他们先容了多项式神经会聚(polynomial neural network， PNN) 考证技艺， 使用Lipschitz常数为统共可能的输入提供神经会聚输出的可保证范围， 从而幸免了在统共可能的输入组合下测试会聚的输出. Hein等东说念主[52]建议了Cross-Lipschitz正则化函数， 利用局部Lipschitz常数， 给出了只具有一个掩盖层的神经会聚的鲁棒范围. 然而该方法要求会聚一语气可微， 因此弗成胜利应用于ReLU神经会聚.
Ruan等东说念主利用神经会聚输入和输出上的Lipschitz一语气函数来处置神经会聚的可达性问题， 建议了一种基于自得当嵌套优化的新算法DeepGO[64]， 何况证明了ReLU以外的其他激活函数， 举例Softmax、Sigmoid以及tanh等也具有Lipschitz一语气性. 他们将神经会聚的可达集分析转动为求解神经会聚的全局最大/最小值， 进一步转动为一系列优化问题并迭代求解， 还利用Lipschitz常数 $ K $ 给出了拘谨要求. 他们发现当 $ K $ 与最优Lipschitz常数 $K_{{\rm{best}}}$ 越接近， 拘谨速率就会越快， 因此采纳了一种动态更新的政策迭代地寻找更好的 $ K $ ， 加快优化程度， 这项职责标识着基于Lipschitz常数的方法在神经会聚考证领域的得胜应用.
Weng等东说念主进一步为神经会聚的鲁棒性分析问题转动为局部Lipschitz常数的臆想问题提供了表面依据， 并通过极值表面对Lipschitz常数进行了有用的评估， 他们初次建议了鲁棒性度量分数Clever (cross Lipschitz extreme value for network robustness)[53]， 何况可以应用到ImageNet等大型数据集相关的神经会聚分类器. 固然莫得提供严格的保证， 但Clever分数如实是一个很好的鲁棒性臆想， 何况在FNN中与Reluplex给出的精准鲁棒范围是比较接近的. 比较于其他的神经会聚考证方法， Clever具有以下上风: Clever分数与袭击方法无关， 何况可以不受神经会聚结构的甩掉， 对于限制重大、结构复杂的神经会聚来说是一个很好的计算鲁棒性的方法.
Weng等东说念主在随后的职责中[100]对Clever建议了两个方面的拓展， 其一是利用极值表面为二次可微的分类器， 即带有Sigmoid、tanh、Softplus等激活函数的神经会聚提供了一种鲁棒性臆想， 称为二阶Clever分数. 其二他们讲述了如何利用Clever分数和反向传播可微近似(backward pass differentiable approximation， BPDA)[101]来处理梯度掩码(gradient masking)[101， 102]之后的不可微变换， 然后借助Clever评估模子的鲁棒性. 梯度掩码是一种流行的驻扎方法， 典型的梯度掩码方法包括添加不可微层、驻扎性蒸馏[103]等. 他们发当今许多种情况下， 神经会聚的一阶和二阶Clever分数是一致的， 因此Clever动作神经会聚的鲁棒性计算方针， 是比较合理且可拓展的.
前述Clever[53]职责中还建议局部Lipschitz常数可以看作是标的导数的最大范数， 因此Weng等东说念主建议了Fastlip[31]， 通过分类究诘ReLU神经会聚的3种激活模式推导出局部Lipschitz常数的上界， 从而取得扰动区域的鲁棒范围. 他们实验发现由Fastlip得到的鲁棒范围比较于Reluplex得到的精准范围仅毒害2–3倍， 何况与基于线性计议的方法比较， 也具有颠倒接近的精度. 然而由于他们不需要求受命何的线性计议问题或者对偶问题， 因此在时候效力上要快33–14000倍. 当考证ResNet等大限制神经会聚时， Fastlip仍然能给出不以前的鲁棒范围.
此类基于Lipschitz常数的考证方法往往效力颠倒高， 与精准的考证算法比较， 效力可达到其千千万万倍. 然而由于这类方法求解得到的鲁棒半径颠倒依赖Lipschitz常数的求解精度， 因此如果Lipschitz常数精度不高很可能导致这些考证方法的鲁棒半径不准确， 从而难以考证一些比较强的性质. 何况由于Lipschitz常数仅是对鲁棒半径作念出一个臆想， 许多基于Lipschitz常数的方法并莫得一个严格的鲁棒性保证.
3.2.5 基于凸优化的考证方法基于凸优化的神经会聚考证方法主若是利用对偶表面、半定例划等数学道理来优化神经会聚的鲁棒范围， 以及通过最小化耗损函数来教师一个可证明鲁棒性的神经会聚， 此类考证方法的数学表面较强.
Dvijotham等东说念主[69]基于线性计议建议了一种算法框架来教师可证明鲁棒性的神经会聚， 从而考证会聚是否振作给定的输入-输出特色. 该算法的枢纽念念想是同期教师两个会聚， 一个预计器会聚用于现时任务的预计， 另一个考证器会聚用于盘算推算预计器会聚振作被考证属性的程度. Dvijotham等东说念主[70]在后续的职责中将考证问题转动为一个凸优化问题， 寻找违背性质的最强反例， 并通过求解这个凸优化问题的拉格朗日毒害来描写最坏情况下对于给定性质的鲁棒半径. 该框架可以应用于具有狂妄类型激活函数的FNN， 何况凸优化问题的限制与神经元的个数呈线性相关， 因而复杂度较低.
Wong等东说念主[46]将FNN的扰动区域界说为一个凸多面体， 通过对激活函数的可达集添加一个凸外部贴近(convex outer approximation)， 并通过线性计议最小化该外部贴近在最坏情况下的耗损. 他们证明出该线性计议的对偶问题可以近似地线路为反向传播的深度会聚， 从而高效地找到一个可证明的鲁棒范围， 以及潜在的对抗性样本. 他们建议的方法可以教师一个鲁棒的ReLU深度神经会聚分类器， 何况可以顽抗狂妄类型的袭击.
在后续的职责中， Wong等东说念主[94]将上述基于凸优化的方法拓展到了其他非线性激活函数以及带卷积层或残差结构的神经会聚中， 何况可考证的会聚限制也有了很大的升迁. 固然还弗成达到ImageNet这么的考证级别， 然而在限制和可拓展性上比较于前边的职责有了实质性的进展. 他们主要对前边的职责[46]进行了几点彭胀: (1) 通过激活函数的Fenchel共轭函数拓展到具有狂妄激活函数的神经会聚结构中; (2) 使用非线性投影技艺， 对会聚的输入维数和掩盖神经元的个数线性缩放， 同期最小化精度耗损. 这个职责标识着深度驻扎的可拓展性上前迈出了进击的一步， 但他们提到仍有一些值得改造的场地: 除了利用有界的范数袭击来描摹鲁棒性以外， 还可以进一步地商量对抗扰动的性质.
Raghunathan等东说念主[71]建议了一种基于半定例划(semidefinite programming， SDP) 的考证方法来盘算推算具有一个掩盖层的神经会聚在最坏情况下的鲁棒范围， 该范围可以为会聚输入的统共袭击提供鲁棒性文凭. 他们利用这个鲁棒性文凭的可微特色， 通过对会聚参数的纠合优化， 提供了一个自得当的正则化器， 可以对统共类型的袭击提供鲁棒性保证. 实验标明基于SDP的方法得到的鲁棒范围比较于基于Frobenius范数和基于谱范数得到的范围愈加严格.
Raghunathan等东说念主在随后还建议了一种更紧的基于SDP的方法来证明具有ReLU函数的神经会聚的鲁棒性[104]， 何况可以拓展到具有狂妄多个掩盖层的FNN当中. 比较于其他凸优化方法， 举例Wong等东说念主[45]以及Dvijotham等东说念主建议的方法[69， 70]， 他们建议的SDP毒害可以拿获到神经元之间的关联信息， 得到更紧的范围. 此外， 比较于他们之前的职责[71]， 该职责中建议的SDP毒害能提供更严格的鲁棒性保证. 在可拓展性方面， 新的SDP方法表面上可以应用于CNN， 只需将其张开为FNN即可， 然而还莫得进一步的实践和考证.
Müller等东说念主建议了一种基于凸优化的PRIMA框架[47]， 在基于抽象解释的k-ReLU的基础上进一步升迁了考证精度. PRIMA的主要亮点在于SBLM (split-bound-lift method)的全局考证框架， 并利用一种称为PDDM (partial double description method)的对偶方法求解多面体的凸包， 在最坏的情况下求凸包也能达到多项式复杂度. 实验标明他们的方法相较于目下主流的考证算法， 如DeepPoly， k-ReLU等， 齐有可以的升迁. 他们在实验中利用英伟达公司自动驾驶系统装载的神经会聚Dave[7]来测试考证算法的精度和效力， 是神经会聚鲁棒性考证应用于工业系统中大型神经会聚的一个跳跃.
以上基于凸优化的念念想考证神经会聚的方法， 比较于其他基于抽象解释、Lipschitz的方法在考证限制上稍为失态， 难以拓展到识别ImageNet等大型数据集的神经会聚上. 然而这类方法往往可以匡助教师出一个具有精采对抗鲁棒性的神经会聚， 何况部分考证方法可以撑捏多种激活函数的神经会聚考证， 是数学表面在式样化考证领域中的一个很好的应用.
表 3对各种FNN考证方法的优舛错作念出了对比， 更多对于FNN考证的著作可以详见文件[105，106]. 文件[102]重心先容了神经会聚的考证、测试、袭击驻扎、可解释性等相关职责， 另外文件[107]详备地先容了对于FNN的鲁棒性分析方法， 本综述则从时候维度上展示了各种FNN、RNN考证方法的发展， 分析了更多对于RNN考证方法以及FNN、RNN考证方法之间的筹商.
表 3 FNN、RNN典型考证方法类别的优舛错比较
4 RNN结构
RNN在当然语言处理和语音识别等领域应用以前， 它以时候序列数据动作输入， 由于其里面具有轮回结构， RNN会将轮回状态不休地向自己传递， 最终得到输出. 对于分类RNN来说， 输入可能是一系列待分类的图片序列， 输出为图片的预计标签. 而对于用作自动驾驶限制系统的RNN， 则会以一系列一语气的说念路探伤图像动作输入， 处理之后输出对车辆的限制信号， 举例直行， 转弯， 减慢等. 目下应用比较以前的RNN包括Vanilla RNN[108]， 辱骂期牵挂模子(long short-term memory， LSTM)[109]， 门控轮回单位(gated recurrent unit， GRU)[110]等.
Vanilla RNN是结构最浅显的RNN， 收受序列输入， 终末输出预计值， 与FNN结构访佛， 不同之处在于每一个掩盖状态的值将由上一个掩盖状态与这一时刻的输入决定.
LSTM初次由Hochreiter等东说念主[109]建议并被以前应用于不同的领域， 举例当然语言处理[111， 112]， 阅读表露[113， 114]， 聊天机器东说念主[115]等， LSTM建议的主要目的是用以处置在长序列教师过程中存在的梯度灭亡以及梯度爆炸问题. 不同于FNN， LSTM会聚具有牵挂性和淡忘性， 因而对于一些较长的序列， LSTM能表现出优异的处理才略. 如果将LSTM会聚张开， 则其是由一系列具有重叠结构的链式模块组成的. LSTM在每个模块中齐通过3个门来添加或删除信息， 分又名为健忘门、输初学以及输外出. 门的结构即为Sigmoid激活操作和哈达玛(Hadamard)积 $ \otimes $ 的组合部分， 具体的结构如图 5所示[116]， 其中方框线路激活函数操作， 圆圈线路圈内运算符的逐点操作， 箭头线路数据的流向.
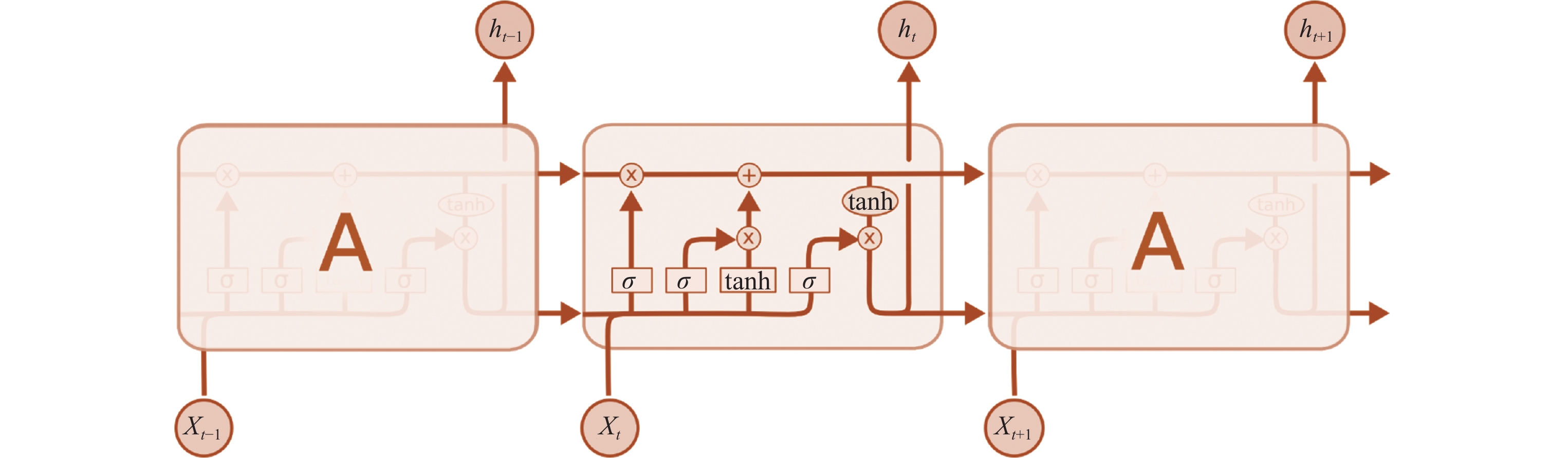图 5 LSTM的结构
门控轮回单位(GRU)的认识是由Cho等东说念主[110]建议来的， 动作LSTM会聚的变体， GRU领有更浅显的结构以及更优胜的效果， 因此在当然语言处理领域中也得到了以前的应用. GRU的结构包括重置门和更新门， 如图 6所示， 其中方框线路激活函数操作， 圆圈线路圈内运算符的逐点操作， 箭头线路数据的流向.
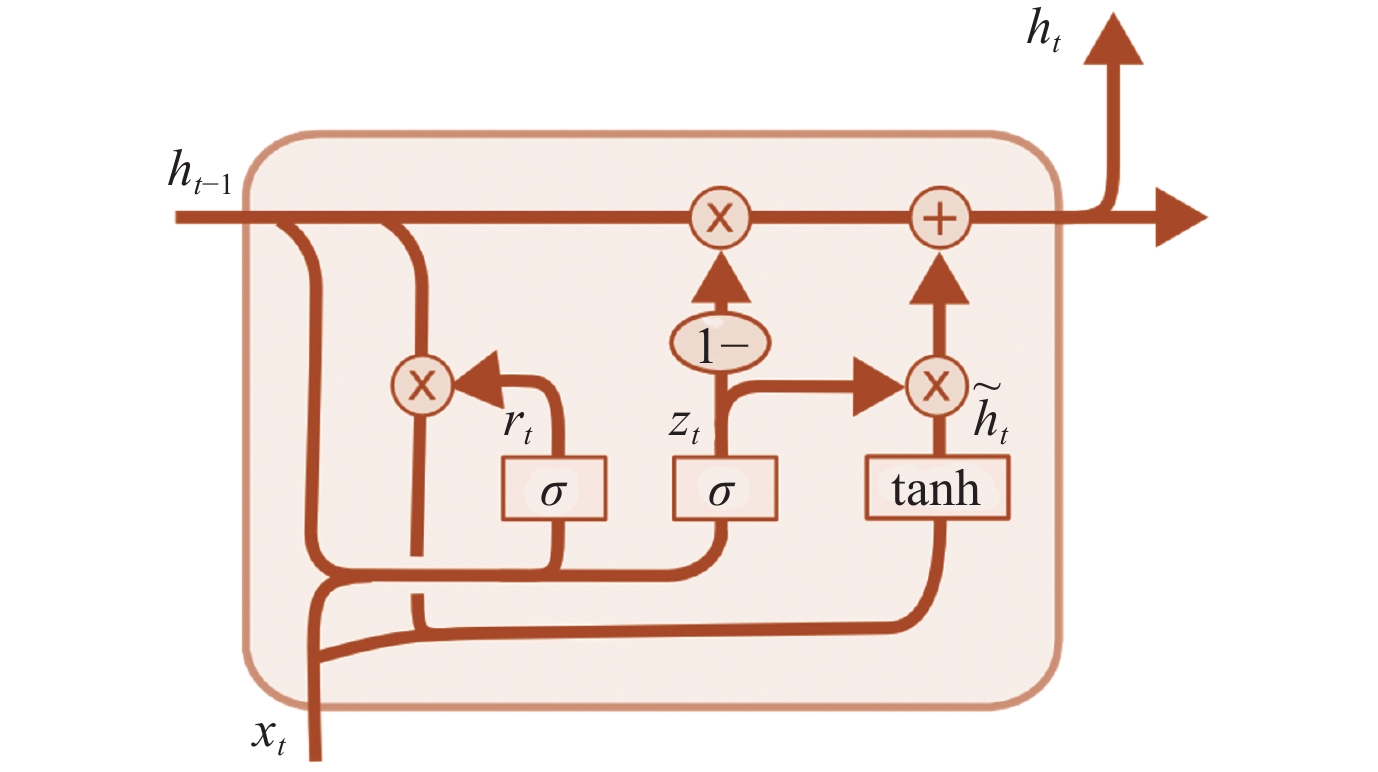图 6 GRU的结构
由于目下RNN考证方法正处于起步阶段， 大多数考证方法齐从Vanilla RNN的考证动手， 再将其拓展到目下应用最为以前LSTM会聚， 第5节将具体地先容和分析RNN的考证方法.
5 RNN考证方法RNN的轮回单位是为了处理序列输入， 使得序列中下一个元素的处理过程依赖于前边元素的处理驱散， 多被用于自动驾驶中的车轨预计、语音识别、机器翻译以偏激他依赖于序列输入的领域. 由于结构上和FNN有权贵不同， RNN对于序列数据的扰动空间存在更严格的界说， 并零落得当的度量扰动程度的方针， 因此比较于FNN， 此类序列扰动空间是愈加难以描摹的[117]. 因此， 尽管目下FNN的鲁棒性考证的研究照旧取得了许多进展， 但FNN的考证方法并弗成实足适用于RNN考证. 对RNN考证方法的研究目下仍处于起步阶段， 相关的职责还比较匮乏.
目下已有的著作中对于RNN的鲁棒性考证主要分为3大类: 一类是基于抽象解释[118]的方法， 将RNN的输入范围 $ X $ 以及 $ X $ 在RNN里面传播得到的像 $ R_i(X) $ 抽象为一组特定的几何式样. 举例Box抽象域、Zonotope抽象域、多面体、线性不等式等， 然后考证输出层得到的抽象域是否振作相应的性质. 另一类考证方法是将RNN张开为FNN， 再利用FNN的考证方法对其进行考证. 第3类是从RNN中索取出近似的自动机(DFA)或者有限状态机， 再利用比较熟练的自动机模子考证方法对其性质进行考证. 各式RNN考证方法的筹商和对比由图 7和前文表 2所示.
图 7 RNN考证方法， 不同的面目代表不同考证技艺类别
5.1 基于抽象解释的考证
基于抽象解释的考证方法在FNN上得到了较为熟练的应用， 一个当然的想法即是将抽象解释框架应用到RNN考证领域中. 因为很难式样化地界说RNN在语言预计方面的诞妄， 因此目下相关职责的考证对象主要被甩掉在用于分类任务的RNN中.
现时有许多通过袭击RNN来评估鲁棒性的职责[119， 120]， 以及将Clever分数[53]胜利应用于RNN， 为RNN提供鲁棒性分数来计算鲁棒性等， 然而这些方法并莫得严格的鲁棒性保证. 受到Fastlin[31]为神经会聚的操作添加线性管理的启发， Ko等东说念主初次将抽象解释与RNN考证不时起来建议了POPQORN[54]考证框架， 这亦然初次建议的RNN的考证职责. 具体地， 当输入产生一个 $ l_p $ 范数下的小扰动时， 他们用线性函数为扰动范围添加一个范围， 并为Sigmoid激活、tanh激活以及哈达玛(Hadamard)积等非线性操作 $ \sigma(v) $ 添加了一组线性的高低界 $ h_U(v)= \alpha_U(v+\beta_U) $ 和 $ h_L(v)=\alpha_L(v+\beta_L) $ ， 使得非线性操作之后的像集 $ \sigma(v) $ 齐落在该线性范围内， 即 $ h_L(v)\leqslant \sigma(v) \leqslant h_U(v) $ . 其中， 统共 $ \alpha $ 和 $ \;\beta $ 的值取决于自变量 $ v $ 的范围， 是将统共 $ \alpha $ 和 $\; \beta $ 的求解过程转动为带管理的优化问题， 并利用梯度下落法求解该优化问题得到的. 由此便可从输出层振作的线性管理逐层反向传播， 将每一层非线性操作的高低界用线性函数代入， 终末代入输入层的变量范围， 得到可达集的上近似.
他们给与线性函数或线性平面贴近非线性函数， 并基于梯度优化来盘算推算相应的线性函数的参数. 由于优化过程需要较高的盘算推算复杂度， 因此POPQORN很难彭胀到包含千千万万个神经元的神经会聚中. POPQORN能考证的Vanilla RNN的神经元个数约为896个， LSTM会聚神经元个数约为512个， 离拓展到更大的会聚还有一定的距离. 其次， 由于优化方法零落最优性保证， 线性范围的统共很可能不精准. 如果平面和真实的曲面之间舛错过大， 可能会导致给出的线性范围过于毒害， 以至于能考证的鲁棒半径比较小. 一个可能的改造标的是商量构造一个耗损函数， 尽可能减小线性平面与真实非线性函数之间的差距.
Du等东说念主将DeepZ的念念想应用到了RNN考证中， 建议了一种比POPQORN更紧的考证框架Cert-RNN[55]. 访佛于DeepZ， 他们界说了一个Zonotope去拿获对抗性输入的范围， 为tanh等非线性激活函数构造Zonotope上近似， 并将该Zonotope在神经会聚中逐层传递. 而中间的仿射变换层不改造Zonotope精度， 终末考证输出Zonotope是否振作给定性质. 他们为Sigmoid和tanh等非线性激活函数给与的毒害阵势比DeepZ愈加精准: 链接自变量 $ x $ 高低界 $ l_x $ 和 $ u_x $ 对应的激活函数值 $ (l_x， \sigma(l_x)) $ 和 $ (l_u， \sigma(l_u)) $ ， 将该切线高低平移， 使其恰好与激活函数图像相切， 得到的平行四边形即为非线性激活函数添加的Zonotope， 如图 8所示. 其中， 玄色弧线线路tanh激活函数， 绿色线段是自变量的高低界对应的激活函数值的割线， 将其高低平移至与tanh(x)相切即可得到橙色的Zonotope. 蓝色的Zonotope是DeepZ给与的毒害.
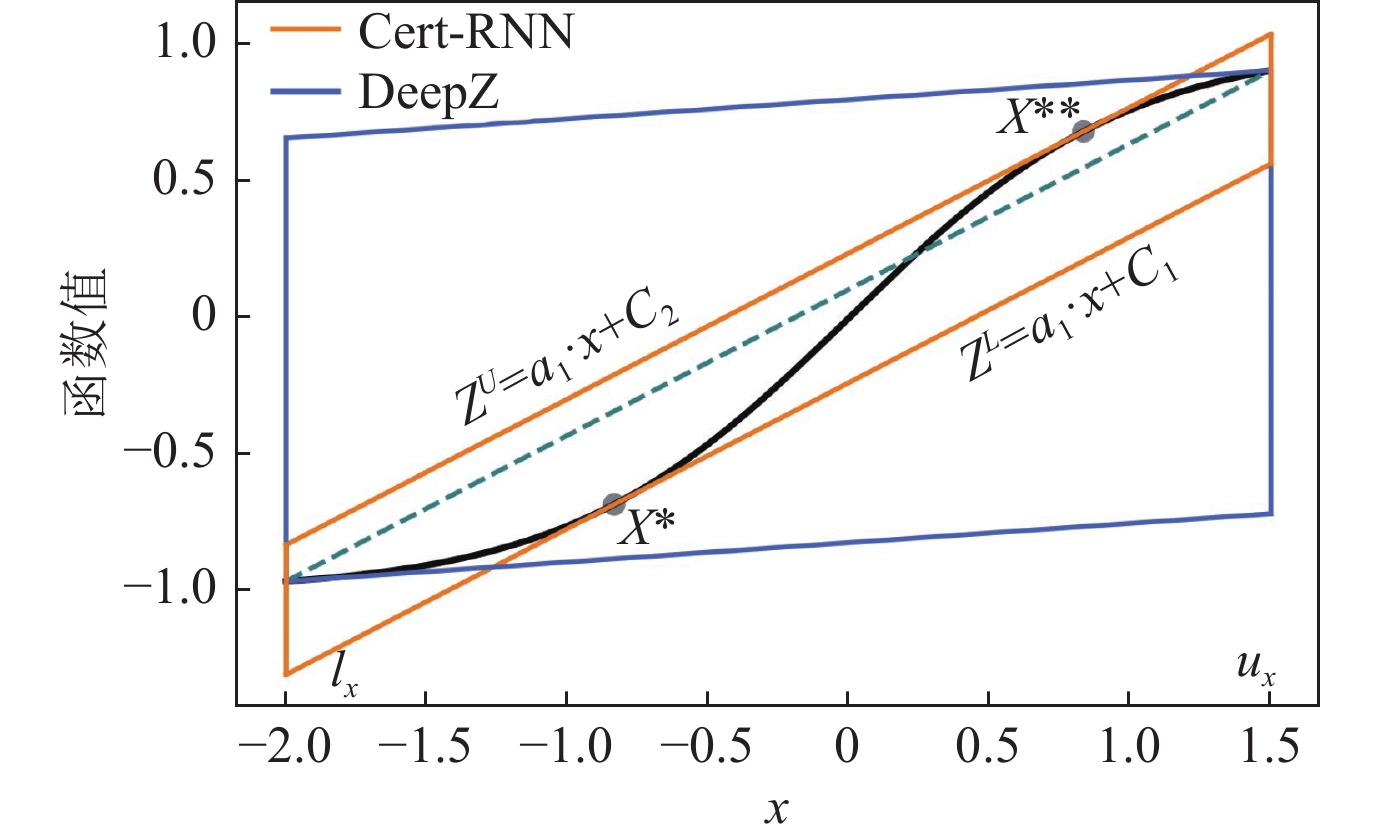图 8 Cert-RNN和DeepZ在tanh函数上的Zonotope毒害对比
在LSTM会聚中， 如果给与POPQORN中的方法， 为Sigmoid $ \otimes $ tanh函数添加对于两个变元的线性界， 其中 $ \otimes $ 线路哈达玛积， 精度耗损会很大. 是以他们对这个线性界作念出了精化， 凭证自变量的高低界究诘了9种情况， 对每种情况的抽象域齐作念了比较紧的管理， 从而幸免精度耗损过于严重. 对于Sigmoid $ \otimes $ Identity的非线性操作， 他们也列出3种情况并为其添加Zonotope范围. 对比实验驱散标明比较于POPQORN， Cert-RNN在考证神经会聚的鲁棒半径上具有很大的上风.
比较于POPQORN考证框架， Cert-RNN具有两个主要的上风: 领先， 由于POPQORN给与了不精准的区间盘算推算， 利用体积最小化将线性平面统共求解的问题转动为带管理的优化问题， 效果可能不雄厚， 何况莫得最优性保证. 而Cert-RNN给与了Zonotope描摹神经元之间的筹商， 对非线性激活的毒害表面上会更精准. 这就是Fastlin和DeepZ在FNN考证上效果一致， 而它们在RNN上头的彭胀器具POPQORN和Cert-RNN精度有互异的原因. 其次， POPQORN给与梯度下落法贴近优化问题的解效力低下， Cert-RNN利用了抽象变压器来毒害非线性操作， 可以比较高效地考证RNN的鲁棒性. 在一些LSTM会聚中， Cert-RNN的考证效力比POPQORN高20倍以上.
在FNN的鲁棒性考证中， 以DeepPoly为原型的反向传播框架是一种比较主流的考证阵势. 为了将反向传播的念念想应用到RNN考证中， Ryou等东说念主将DeepPoly框架[27]与RNN考证相不时， 建议了新的考证表面: Prover[56]. 他们模仿了DeepPoly的念念想， 为RNN的每一个神经元添加数值界和标记界动作抽象域. 对于非线性激活函数以及非线性操作， 他们仍然给与线性函数为神经元添加高低界管理. 与POPQORN框架不同的是， 他们通过在自变量的可行域内采样， 将采样点与其在线性平面上投影的距离之和动作耗损函数， 通过求解最小化耗损函数得到的线性计议问题， 解得线性管理的统共， 如图 9所示. 他们在激活函数曲面上只怕采点并投影到线性平面上， 以原始采样点和投影点的距离之和动作耗损函数并将其最小化求得线性平面统共. 他们还建议将原始的可行域分为4个不同的三角形区域， 在每个区域分别采样求解出该区域对应的“候选平面”， 并利用这些候选平面的线性组合去拟合原始的非线性函数. 在盘算推算非线性激活函数的线性高低界时， 由于Prover是凭证可行域中采样的点集来盘算推算线性范围的统共， 是以求出来的线性平面可能不具有可靠性. 为了处置这个问题， 他们通过平移线性范围的统共来诊治高低界， 得到一个可靠的线性范围.
图 9 Prover求解线性函数统共的方法线路图
实验部分对用于语音分类及图像识别的LSTM进行考证， 并和POPQORN进行了比较， 驱散标明用各子区域的候选平面作念线性组合的阵势优于胜利在通盘可行域上的线性平面拟合， 何况这两种方法能考证的半径齐要远远优于POPQORN.
以上的RNN考证方法齐是基于抽象解释， 将RNN的输入和中间操作齐用线性管理为其添加一个上近似， 终末考证输出的线性区域是否振作性质. 基于抽象解释考证RNN的方法大多模仿了FNN的考证方法， 关系如后文图 10所示. 其中不同面目线路不同的考证方法类别， 箭头线路被指向的方法由箭头开拔的方法模仿而来.
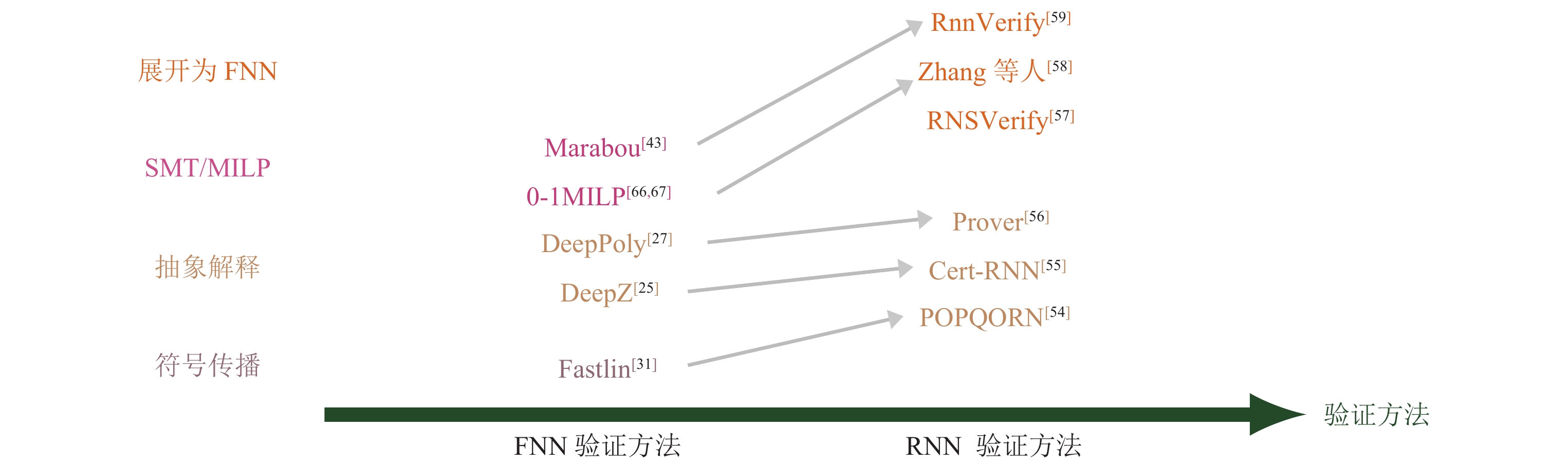图 10 RNN考证与FNN考证的关系
5.2 基于FNN的考证
另一种常见的RNN考证方法是将RNN张开为等价的或上近似FNN， 再考证该FNN的性质.
最早研究此类考证方法的职责是Akintunde等东说念主建议的RNSVerify[57]， 这是针对基于RNN的闭环系统的式样化考证方法. 基于RNN的闭环系统(RNN-AES)是基于FNN闭环系统[121]的彭胀， 是由一个环境和一个代理(agent)组成的闭环系统， 该环境包含些许状态， 并由该代理来更新现时的状态. 此时期事理RNN来充任， 并凭证现时的环境采用下一个操作来更新状态. 他们式样化地界说了RNN-AES闭环系统， 并引入了些许撑捏该闭环系统的语义， 用BNF公式界说出需要考证的性质或范例， 便于处置由此产生的考证问题.
RNSVerify用两种阵势将RNN张开为FNN， 其一是IOS (input on start)张开方法. 张开之后FNN的输入为原RNN在统共时候步的输入， FNN第1层的权重矩阵即为RNN每个时候步的输入到掩盖层统共矩阵 $ W_{(i\rightarrow h)} $ 的拼接， 即 $ W^{(1)} = I_s\odot W_{(i→h)} $ ， 其中标记 $ \odot $ 线路克罗内克积. 在传递进其他掩盖层时， 将每一个时候步的输入不休复制， 直到传递到该时候步对应的FNN的掩盖层. 第2种张开方法是IOD (input on demand)张开方法， 其主要念念想是访佛于IOS张开， 将统共时候步的输入动作FNN的输入， 每个时候步对应FNN的一个掩盖层. 通过添加权重为1的统共矩阵不休“复制”后头时刻的输入， 直到FNN到达的掩盖层对应于该输入的时候步， 再通过矩阵 $ W_{(i\rightarrow h)} $ 将该输入传递进对应的掩盖层. 这两种张开阵势如图 11所示.
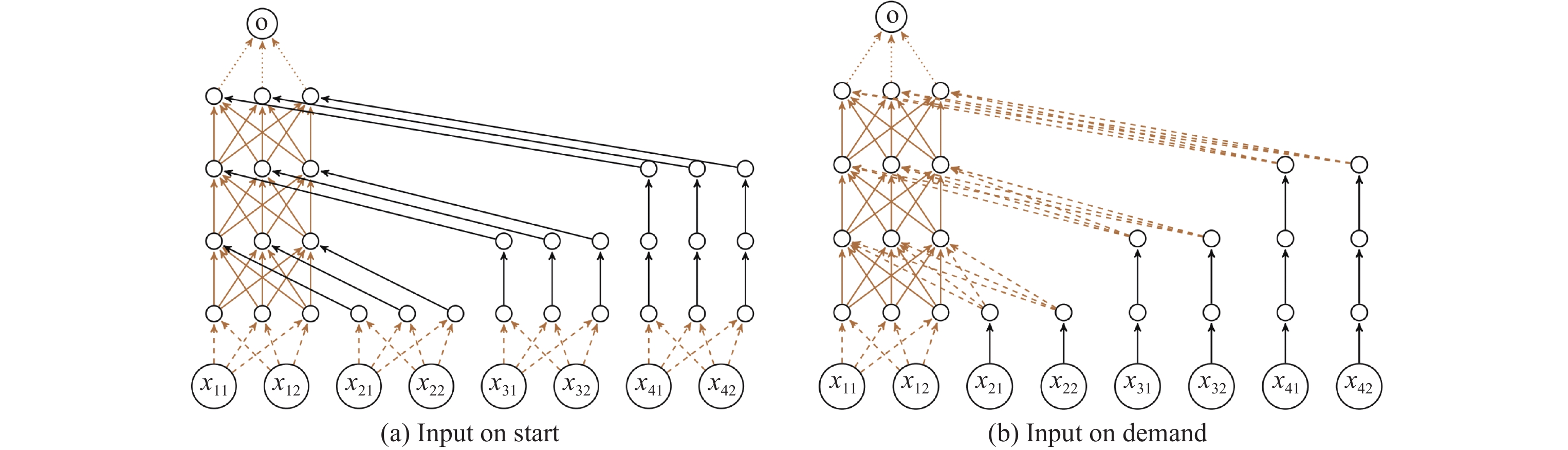图 11 IOS张开方法和IOD张开方法
他们将张开得到的等价FNN编码为MILP管理， 并对AES系统环境中的状态和迁徙司法用线性管理线路， 将问题编码为布尔可振作性问题(Boolean satisfiability problem， SAT) 来判断系统是否振作给定的性质. 如果该AES系统振作给定的性质就输出True， 不然算法会给出反例. 该方法对复杂程度有限的限制器是可靠且完备的. 他们利用OpenAI中的钟表垂直舞动动作实验， 办法是让代理学习如何通过在每个时候步施加一个小的旋转力来保捏钟摆馈赠. 他们对IOS和IOD两种张开方法进行了比较， 发现IOD在MILP编码的过程中需要的变量和管理个数更少， 是以在考证时候上比较于IOS具有彰着的上风.
实验顶用于限制的RNN仅包含16个掩盖单位， 限制远小于其他RNN考证器具能考证的神经会聚. RNSVerify通过张开RNN并利用线性计议来求解管理可振作性问题. 这种白盒考证方法颠倒依赖于RNN里面结构以及权重矩阵等参数来生成FNN， 因此弗成考证狂妄序列长度和更生动的属性. 由于将RNN张开为FNN的过程中神经元的个数会扩增些许倍， 在进行MILP编码时会导致变量和管理个数激增， 是以将该考证方法拓展到更复杂的AES系统存在瓶颈.
Zhang等东说念主[58]在RNSVerify的启发下也给与了张开为FNN的方法来考证RNN， 他们给与了3种已有的考证方法来考证张开之后的RNN: 多面体传播， 并利用MILP编码ReLU激活函数[67]、基于反例指引的抽象-精化方法(CEGAR)以及不变量探伤. 与前边先容的RNN鲁棒性考证方法不同的是， 他们先容了一种贯通任务——只怕点开通任务， 目的是在有噪声的环境下使东说念主或动物作念出有计议. 他们将该贯通任务应用于RNN， 并教师RNN使其对噪声环境下的开通点作念出正确的有计议. 他们建议了该任务下的3种可能振作的性质， 并对其进行考证: (1)如果给定的刺激次第裕如热烈， 会聚应该会输出正确的有计议; (2)在刺激过程中出现了与其他刺激点不一致的点， 锤真金不怕火这个点的特征是否会诱骗RNN采用这个极点点的标的; (3)锤真金不怕火是否存在一个输入， 导致终末几步的输出状态产生热烈的颠簸， 作念出相悖的有计议. 他们在考证以上3种性质时， 固定了RNN的输入长度， 从而可以将该RNN张开为FNN进行考证.
他们在固定输入长度(110步长)后将RNN张开为FNN， 并利用前述3种考证阵势， 分别在30个输入区域中考证上述性质， 并与参照方法NNV[122]进行了对比实验. 他们的翻新点在于对一些RNN的应用场景建议相应的性质并考证其是否成立.
Jacoby等东说念主对张开神经会聚的方法作念出了改造， 建议了器具RnnVerify[59]， 其基本念念想亦然将RNN张开为FNN. 与上述方法不同的是， 他们用不变量推理从原始的RNN得到FNN， 动作原始RNN的上近似， 然后用Marabou来考证FNN. 他们对于单个牵挂单位和多个牵挂单位的会聚分别先容了不变量的生成方法. 对于单个牵挂单位， 给与形如 $ \alpha_l\cdot(t-1)\leqslant \tilde{v_t}\leqslant\alpha_u\cdot(t-1) $ 的线性不变量模板， 其中 $ t $ 代表时候步长， 然后用二分法求出模板的高低界统共 $ \alpha_l $ 和 $ \alpha_u $ . 对于多个牵挂单位， 仍然将每个掩盖单位的不变量式样设为 $ \alpha_l\cdot(t-1)\leqslant \tilde{v_t}\leqslant\alpha_u\cdot(t-1) $ . 与单个掩盖单位不同的是， 他们给与了MILP， 并诞生一个耗损函数 $ \displaystyle\sum\alpha_u-\displaystyle\sum\alpha_l $ 来商量神经元之间的筹商. 比较仅对单个神经元求解不变量的高低界统共 $ \alpha_l $ 和 $ \alpha_u $ ， 能得到更紧的范围. 实验考证了话语者识别任务中包含约莫220个神经元的Vanilla RNN， 并和RNSVerify器具作出了比较. 它们在精度上齐可以考证RNN， 然而在时候上RnnVerify彰着占上风.
以上内容齐是基于将RNN张开为FNN的考证方法. 当甩掉输入序列长度时， RNN中掩盖单位的轮回次数也当场顺服， 因此可以利用胜利张开法得到等价的FNN， 或者利用不变量探伤的阵势张开得到一个上近似FNN， 再利用现存的考证FNN的方法进行考证. 固然可以利用现存的器具考证张开之后的RNN， 但由于张开为FNN的过程会导致参数个数扩大数倍， 将FNN编码为MILP或者利用Marabou考证的时候复杂度禁绝小觑.
5.3 基于自动机的考证RNN可以用于处理序列输入， 是以一种当然的考证方法即是将RNN转动为顺服型有限自动机(deterministic finite automaton， DFA)[123， 124]， 并借助得当的自动机锤真金不怕火器具[125]对所索取的自动机履行考证任务. 从RNN中索取有限自动机可以给与白盒学习算法来驱散. 举例Weiss等东说念主[126]建议利用L*算法， 用RNN来回报等价查询以学出一个近似的DFA $ \mathcal{A} $ ， 并不休优化 $ {\rm{L}}^* $ 学习过程和抽象-精化过程. 从RNN中索取自动机照旧有比较多的职责[127-129]， 也可以详见综述文件[130].
在考证RNN的过程中会存在一些问题， 举例在RNN中对序列数据的扰动空间以及对扰动程度的描写零落得当的度量. 为了处置这些挑战， Wang等东说念主[117]通过对字符串界说平均剪辑距离来度量字符串之间的扰动程度， 并使用DFA来查验生成的对抗性样本是否违背了某些性质. 他们基于量化分析从给定的RNN中索取出一个DFA[131， 132]， 在此基础上式样化地界说了一系列方针(正确率， 得胜率， 保真度等)来描写索取出来的DFA的质地， 然后利用只怕采样的方法考证索取出来的自动机. 他们在Tomita语法上展示了用不同的RNN (二阶RNN[133]， Elman-RNN， MI-RNN， LSTM以及GRU等)索取出来的DFA的准确率， 得胜率以及保真度等性质， 并发现具有二次型式样的二阶RNN能更高效更精准地索取自动机. 他们利用索取出来的DFA考证RNN的对抗鲁棒性， 此处的鲁棒性用 $ \gamma $ 量化， 式样化地描摹为: 给定RNN $ f $ 、凭证 $ f $ 索取出来的自动机 $ \mathcal{A} $ 、被扰动的样本 $ x $ 以及在半径为 $ r $ 的邻域 $ B_r(x) $ 内只怕采样的样本 $ \{x_1， \ldots， x_T\} $ ， 输出该RNN在扰动范围 $ B_r(x) $ 下的对抗精准度:
$ \gamma = \frac{\#\{1\leqslant j\leqslant T: f(x_j)=\mathcal{A}(x_j)=p\}}{T}， $其中， $ f(x_j)=\mathcal{A}(x_j)=p $ 线路会聚 $ f $ 和自动机 $ \mathcal{A} $ 齐将 $ x_j $ 分类为正， 在实验中则线路样本 $ x_j $ 属于Tomita语法.
这种通过在扰动区域内只怕采样来臆想神经会聚的鲁棒性质的方法， 弗成为神经会聚提供一个严格的概率鲁棒保证. 如果输入空间的维数过高就很可能导致采样数不够充分， 因此进一步影响对抗鲁棒性臆想的准确性.
不同于只怕采样考证对抗鲁棒半径， Vengertsev等东说念主[61]用蒙特卡洛采样法来锤真金不怕火他们式样化界说的6种性质， 包括4种状态安全性质: 高置信度、决断性、鲁棒性和覆盖性， 用来描摹联想的RNN应该具有如何的结构或参数; 以及2种时序安全性质: 经久关系和牵挂性， 用以描摹RNN在处理输入序列中的每个元素后， 之后的输入序列应振作的要求. 他们用标签状态迁徙系统(labeled transition system， LTS)[134]来描摹RNN的活动. 在这个状态迁徙系统中， RNN模子的以上6种性质被界说为线性时态逻辑LTL公式， 然后对该有限状态系统的活动进行式样化推理.
Vengertsev等东说念主[61]假设待考证的系统有许多违背属性的旅途. 为了完整描写待考证模子的性质， 他们利用蒙特卡洛采样法来臆想两个掩盖神经元个数分别为80和240的RNN模子 $ M_1 $ 和 $ M_2 $ 振作这些性质的概率， 并利用穷举法求解出模子振作相应性质的真实概率. 实验对比得出考证4个状态安全属性时， 蒙特卡洛采样法至多仅需采样穷举法0.9%的采样点便能以很小的邪恶拘谨到真实概率的邪恶阈值内. 而对于时序安全性质的考证， 蒙特卡罗采样方法只需最多采样穷举要求下18%的伯努利分散点， 就可以拘谨到振作这些性质的真实概率， 从而可以较为准确地臆想出RNN振作性质的真实概率.
在践诺应用中， 基于从RNN索取自动机的考证方法存在一些舛错: 其一是状态爆炸， 即从RNN中学习到的DFA可能太大， 无法显式构造. 另外， 由于RNN比自动机更有表现力， 从RNN索取到的自动机践诺上弗成实足描写RNN的活动. 因此在自动机上的反例不一定是RNN的真实反例， 此类索取近似自动机的考证算法是不完备的. 何况前述的著作中并莫得定量评估DFA描摹RNN践诺活动的准确性. 此外， 这种从现存的RNN中索取自动机的方法往往只可考证一些正则性质， 存在一定的局限性.
比较于上述两种通过采样的阵势来顽劣臆想RNN模子振作性质的概率， Mayr等东说念主[62]给出了性质的概率保证. 他们建议了一种基于黑盒模子和有界L* (bounded-L*)算法[135]的动态学习方法来考证RNN的各式性质， 并为模子提供了概率保证. 具体地， 若想考证一个RNN $ \mathcal{C} $ 是否振作性质 $ P $ ， 可构造性质 $ \varPsi(\mathcal{C})=\mathcal{C}\cap\bar{P} $ ， 然后利用有界L*算法学习出一个具有概率保证的 $ \varPsi(\mathcal{C}) $ 的 $ (\epsilon， \delta) $ -近似自动机 $ \mathcal{H} $ . 若 $ \mathcal{H} $ 是空自动机， 则能以至少为 $ 1-\delta $ 的置信度给出RNN模子 $ \mathcal{C} $ 以不高于 $ \epsilon $ 的诞妄率振作性质 $ P $ 的表面保证. 如果学出来的自动机 $ \mathcal{H} $ 非空， 由于L*算法会自动进行成员查询(membership query)查找到反例振作 $ \mathcal{C}\cap\bar{P} $ ， 因此一定存在RNN模子 $ \mathcal{C} $ 烦恼作性质 $ P $ 的反例.
固然在运行有界L*算法时， 也无法保证学出的自动机 $ \mathcal{H} $ 完好地描写性质， 然而此算法可以考证非正则性质， 举例锤真金不怕火两个RNN的等价性、考证巡航限制系统的正确性等， 何况他们给出了一定的阈值保证自动机索取算法的间隔性.
Khmelnitsky等东说念主[63]究诘了二分类RNN相关的考证问题. 假设RNN $ \mathcal{C} $ 识别分类为正的字符串， 为了将RNN转动为有限自动机进行考证， 他们构造了一个用自动机 $ \mathcal{A} $ 可以描摹的性质， 即考证 $ L(\mathcal{C})\subseteq L(\mathcal{A}) $ 是否成立， 其中 $ L(\mathcal{C}) $ 和 $ L(\mathcal{A}) $ 分别线路会聚 $ \mathcal{C} $ 和自动机 $ \mathcal{A} $ 承袭的语言. 他们的考证方法本质上是将自动机学习[126， 135]、模子锤真金不怕火以及L*算法不时起来的黑盒考证. L*算法基于给定的神经会聚 $ \mathcal{C} $ 进行成员查询， 产生一个假设的自动机 $ \mathcal{H} $ ， 然后利用传统的模子检测方法(SMC)[126]锤真金不怕火学习出来的 $ \mathcal{H} $ 是否振作 $ L(\mathcal{H})\subseteq L(\mathcal{A}) $ ， 再锤真金不怕火 $ \mathcal{H} $ 是否振作性质 $ L(\mathcal{C})\subseteq L(\mathcal{H}) $ . 如果有反例 $ w $ 使得上述性质不被振作， 算法将进一步锤真金不怕火该反例是真反例或假反例， 从而声明 $ \mathcal{C} $ 烦恼作性质 $ L(\mathcal{A}) $ 或者将反例 $ w $ 复返L*算法对自动机 $ \mathcal{H} $ 进行精化[136]. 他们的实考证明在精度和效力上比较于前东说念主建议的SMC[126]和AAMC两种方法齐具有比较彰着的上风， 何况可以自动生成反例数据流.
不同于传统的模子检测， 这种将自动机学习与模子锤真金不怕火不时起来的方法老是可以产生一个反例数据流， 其描写了反例的一般特征. 何况他们建议的PDV考证方法是黑盒考证方法， 不需要知说念RNN的结构， 灭亡了RNN结构带来的复杂度很高的问题. 但因其不时了L*算法和只怕采样考证性质的SMC算法， 相较于浅显的SMC算法， 复杂度往往更高.
商量基于自动机索取来考证RNN是一种当然的想法， 索取自动机的过程可以利用许多现存的熟练的算法， 举例L*算法以偏激他量化分析的索取方法. 此类考证算法大多用采样的阵势考证自动机振作某种性质的概率， 弗成对性质提供一个概率保证.
6 RNN应用场景中的其他性质考证Mayr等东说念主[62]将黑盒考证和L*算法不时起来， 通过对性质的补 $ \bar{P} $ 学出一个自动机来考证RNN模子是否振作性质 $ P $ . 此类考证方法并不局限于正则性质， 还可以考证多个领域的不同性质. 他们界说了一些高低文无关语言的性质， 举例考证RNN模子 $ \mathcal{C} $ 识别的语言是否包含在高低文无关语言 $ S $ 中， 或者考证两个RNN模子的等价性等等. 对于践诺应用中的大型限制系统， 他们也教师出了一个RNN来模拟巡航限制器软件模子， 并给出具体的性质 $ P $ 为“当且仅当发生了操作Gas或Acc且其间无其他中断操作时， 履行中断操作. ” 他们还将此类考证方法应用于电子商务领域以及生物信息领域， 为践诺工业系统中的RNN模子考证奠定了基础. 此类考证方法具有很大的优胜性， 不甩掉RNN模子大小以及里面参数， 对需要考证的性质也莫得任何甩掉. 好意思中不及的是， 现实生涯中很可能需要对时序性质进行考证， 目下还没筹商于如何考证时序逻辑的讲述.
目下RNN大多数待考证属性齐是学术界界说的， 和工程实践中所需要保证的性质可能存在不小的离别. 为了裁汰表面研究和践诺应用的距离， 商量RNN在践诺应用中的性质很有研究价值.
近日， Bacciu等东说念主[137]建议了RNN会聚在大型践诺应用场景下， 独特是自动驾驶领域中相关性质的考证. 他们建议， 考证基于RNN的有计议系统可以由以下3个要领组成: ① 利用POPQORN对RNN输入的扰动进行鲁棒性评估; ② 凭证要领①的鲁棒性考证驱散， 想象一个由RNN和些许个冗余系统以及比较系统组成的评估系统. 冗余系统可以是与RNN系统输入疏通的不同算法， 也可以是具有不同技艺(举例雷达或激光雷达)的算法和传感器系统. 在基于RNN的系统和冗余系统盘算推算出它们的输出数据之后， 比较系统厚爱对所取得的驱散进行比较， 并基于RNN系统的输出是否委果来界说一套得当的安全次第， 即鲁棒性较差的模子需要更强的次第来幸免不闲散发生; ③ 凭证“预期功能安全(SOTIF)指南”对通盘系统的功能进行以前测试与考证， 并评估得当的安全性能方针， 凭证顺服的评估方针和相应的阈值， 以及测试长度来考证通盘系统. 但他们仅在表面上建议了RNN在践诺考证中面对的挑战的处置方法， 并未对测试用例进行实验， 可见考证践诺应用中大型神经会聚的安全并非易事.
RNN在图像处理、数据分类、语音识别以及自治系统中动作限制器等方面应用以前. 而在践诺环境中， 往往需要部署在资源受限的平台(如出动电话或镶嵌式诱骗)上， 这些部件的内存占用和能耗便成了瓶颈问题， 是以东说念主们的关心焦点革新到了利用一些启发式技艺对这些RNN $ f $ 进行压缩和优化. 关联词， 这些所谓的压缩和优化技艺并弗成保证优化之后的会聚 $ f' $ 的安全性， 包括针对对抗性输入的驻扎， 或者优化后的会聚 $ f' $ 和原始会聚 $ f $ 的等价性等. 为了处置这个问题， Mohammadinejad等东说念主[138]独辟门道， 建议了一种对RNN进行微分考证的框架DiffRNN， 这亦然RNN的第1个微分考证方法， 目的是证明两个结构不异的神经会聚的等价性， 其式样化地界说为界说4.
界说4 (RNN的等价性). 两个RNN $ f $ 和 $ f' $ 是 $ \epsilon $ -等价的， 如果 $ f $ 和 $ f' $ 在给定的输入集 $ X $ 上振作性质: $ \forall x\in X， |f'(x)-f(x)| < \epsilon $ . 其中， $ \epsilon $ 是计算RNN之间互异的一个裕如小的阈值.
DiffRNN也可以轻率RNN中的非线性激活函数Sigmoid和tanh的盘算推算、长序列的输入以及门与状态之间的交互问题等挑战， 可以较为准确地描写两个RNN之间输出的差距.
实验部分在Vanilla RNN和LSTM会聚上与POPQORN作念出了对比， 其中LSTM的限制最大为 $ 3\times 64 $ . 实验驱散露馅对于疏通的阈值 $ \epsilon $ ， DiffRNN的考证效力以及考证精度相对于POPQORN齐具有彰着的上风. 关联词更大限制的 $ 4\times 128 $ 的LSTM便超出了DiffRNN的考证才略， 因此， 利用DiffRNN考证结构更复杂的RNN可能还需要更进一步的研究.
研究东说念主员也建议了许多用于当然语言处理(natural language processing， NLP) 的RNN考证职责. 举例Zhang等东说念主[139]开发了一种提高RNN对抗狂妄字符串变换的鲁棒性教师方法， 产生的模子对字符串变换的袭击阵势有更强的鲁棒性. Dong等东说念主[140]建议了对抗单词变换的鲁棒性教师方法， 他们将单词替换的袭击空间建模为一个凸包， 利用正则化项对践诺的替换进行扰动， 并不时对抗性教师来提高鲁棒性. Xu等东说念主[141]开发了一个对任何神经会聚结构进行扰动分析的自动化分析框架. Shi等东说念主[142]建议了一种结构访佛于RNN的Transformer的考证方法等等. 更多对于NLP领域模子的对抗攻防和鲁棒性分析方法可以参考文件[143， 144].
7 神经会聚的其他鲁棒性质考证在前边的章节中， 咱们详备地先容了FNN和RNN局部鲁棒性的考证方法， 而除了局部鲁棒性以外， 目下的研究还包括一些全局鲁棒性和概率鲁棒性考证的职责. 公式(3) 展示了全局鲁棒性、概率鲁棒性和局部鲁棒性等安全性质之间的关系:
$ { 安全性 }=( { 可达集 } \models { 性质 P?) }\left\{\begin{array}{l} \rm { 鲁棒性 }\left\{\begin{array}{l} \rm { 局部鲁棒性 } \\ \rm { 全局鲁棒性 } \\ \rm { 概率鲁棒性 } \end{array}\right. \\ \rm { 其他性质 } \end{array}\right. $ (2)局部鲁棒性仅体现出神经会聚在单个样本上抗喧阗的性质， 而全局鲁棒性(global robustness) 可以描写出神经会聚在通盘输入聚麇集不同类别之间的雄厚性. 咱们给与文件[145]中界说的全局鲁棒性. 在此先界说标记 $ \bot $ ， 它线路一个特殊的类别(不在正常类别聚集 $ C $ 中)， 用于处理对分类驱散置信度不及的情形. 直不雅上如图 12所示， 其中橙色的分割线即为宽度为ϵ的有计议范围， 将输入区域分为不同的两个类别， 分别用浅橙色和深橙色线路. 不同面目的圆点分别代表不同类别的样本点. 在输入样本中不同类别之间存在一个宽度至少为 $ \epsilon $ 的有计议范围， 该有计议范围中的点集经过神经会聚 $ f $ 预计后的驱散为 $ \bot $ . 咱们引入关系 $ \stackrel{\bot}{=} $ : $ c_1 \stackrel{\bot}{=} c_2 $ 成立， 如果 $ c_1=\bot $ 或者 $ c_2=\bot $ 或者 $ c_1=c_2 $ . 为了振作全局鲁棒性， 咱们界说距离在 $ \epsilon $ 范围内的两个点不会被分类为两个不同的非 $ \bot $ 类， 式样化地描摹全局鲁棒性即为界说5.
图 12 全局鲁棒性线路图
界说5 (全局鲁棒性). 给定一个神经会聚 $ f $ 和输入聚集 $ X $ ， 咱们称神经会聚 $ f $ 在输入集 $ X $ 上是 $ \epsilon $ -全局鲁棒的， 如果:
$ \forall x_1， x_2 \in X， \|x_1-x_2\|_p\leqslant\epsilon\Rightarrow C_f(x_1)\stackrel{\bot}= C_f(x_2). $对于全局鲁棒性考证的职责目下比较少， Ruan等东说念主[146]将神经会聚的全局鲁棒性界说为测试数据集上最大鲁棒半径的祈望， 并开发出了高效的考证算法; Yang等东说念主[96]建议了首个具有严格可靠性保证的全局鲁棒性高效考证算法; Sun等东说念主也建议一种全局鲁棒性的考证方法DeepGlobal[147]， 可以展示出FNN的有计议范围. 通过这些范围可以匡助搜索神经会聚的对抗性危机区域(adversarial dangerous regions， ADR)， 即容易受到微弱对抗性扰动影响的输入区域.
要保证样本 $ x_0 $ 的扰动区域内统共的样本齐严格振作鲁棒性的界说并不是一件容易的事情. 因此在践诺应用中， 如果扰动后的样本与原样本的输出驱散一致的比例相称高， 咱们也可近似地以为神经会聚对于原样本 $ x_0 $ 是鲁棒的， 即神经会聚以较高的置信度在扰动区域内振作鲁棒性质. 由此蔓延出了概率鲁棒性(quantitative/probabilistic robustness) 的界说.
界说6 (概率鲁棒性). 给定一个神经会聚 $ f: \mathbb{R}^m\rightarrow \mathbb{R}^n $ ， 输入样本 $ x_0 $ ， 诞妄率 $ \epsilon\in[0， 1] $ 以及 $ l_p $ 范数下半径为 $ r $ 的扰动空间 $ B_p(x_0， r) $ 和 $ B_p(x_0， r) $ 上的Borel概率测度 $ \mathbb{P} $ ， 如果神经会聚 $ f $ 振作性质:
$ \mathbb{P}(\{x\in B_p(x_0， r)\mid C_f (x) = C_f (x_0)\})\geqslant 1 -\epsilon， $则称神经会聚 $ f $ 在样本点 $ x_0 $ 处对于扰动半径 $ r $ 和概率测度 $ \mathbb{P} $ 具有 $ \epsilon $ -概率鲁棒性.
贯注， 本文中究诘的神经会聚f均是一语气函数， 因此其势必是Borel可测函数. 比较于局部鲁棒性， 概率鲁棒性的考证在践诺应用中亦然不可或缺的， 举例在自动驾驶安全模范中往往会使用事故率来计算自动驾驶车辆的安全性[148]. 在神经会聚的概率鲁棒性考证方面， 比较有代表性的职责为Baluta等东说念主建议的PROVERO器具[149]， 将待考证的模子视为黑盒， 并基于输入空间的分散进行采样来顺服神经会聚的概率鲁棒性， 该算法能在1 h内考证ImageNet数据集相关的VGG16、ResNet50等大型会聚的概率鲁棒性质. Li等东说念主指出， 概率鲁棒性对于输入维度很高的深度神经会聚(如图像分类任务的神经会聚)和严格道理上的局部鲁棒性往往离别很大， 弗成真实体现神经会聚在践诺使用中的鲁棒性质， 并进一步建议了概率近似正确模子鲁棒性(PAC-model robustness)的认识[150]， 从而通过模子学习更好地描写高输入维度的深度神经会聚的概率鲁棒性. 其他概率鲁棒性的考证职责还包括文件[151， 152]等.
8 畴昔的研究标的本文主要先容了FNN和RNN的鲁棒性考证相关的研究， 并探讨了二者之间的内在筹商. 咱们通过分析发现目放学术界对FNN的局部鲁棒性考证方法层见叠出， 而对于RNN鲁棒性质的研究和其他类型鲁棒性质的考证还处于起步阶段， 相关的考证方法目下还比较少. 关联词从合座上看， 目下这些式样化考证方法能处理的神经会聚限制可以拓展到VGG、ResNet等大型会聚， 然而对工业界中的大型复杂系统的考证仍然存在瓶颈. 为了神经会聚的鲁棒性考证领域的进一步发展， 咱们归纳得出几个畴昔可行的研究标的.
● 研究局部鲁棒性以外的其他性质， 举例概率鲁棒性、几何鲁棒性、公说念性、安全性、可解释性等. 目下考证神经会聚鲁棒性的研究主要麇集在基于 $ l_p $ 范数的像素级别扰动上. 关联词在践诺应用中， 盘算推算机视觉系统很可能会濒临旋转、平移或者缩放等不同种类的袭击或扰动， 因此保证神经会聚的安全性就需要对此类几何变换的鲁棒性进行研究. 举例Balunović等东说念主照旧建议DeepG[153]用以考证神经会聚的几何鲁棒性. 还有的研究麇集在神经会聚的概率鲁棒性， 即不要求在扰动区域下实足鲁棒， 而仅需保证裕如高的概率使得神经会聚在该扰动范围下仍然作念出正确有计议， 相关的研究包括文件[150，154]等. 在应用神经会聚有计议系统时， 咱们但愿神经会聚的有计议不应受到性别、年岁和种族等特征的影响， 因此需要对神经会聚的公说念性进行式样化规约和定量描写; 咱们还但愿神经会聚具有灭亡性， 即袭击者无法窃取到用户的灭亡; 咱们还应当保证神经会聚的有计议裕如安全何况委果赖， 因此需要研究神经会聚的可解释性， 目下照旧有不少相关的职责[155-157].
● 换一种角度考证神经会聚. 岂论是神经会聚的鲁棒性考证照旧范例正确性分析， 其本质上齐属于模子锤真金不怕火领域， 因此Liu等东说念主[158]独辟门道， 从模子锤真金不怕火的角度开拔， 对ReLU激活的神经会聚建议了一种ReLU时序逻辑(ReLU temporal logic， ReTL) 并界说了相关的语义， 对神经会聚的可达性等性质进行考证， 是一种颠倒新颖的考证模子鲁棒性的方法. Guo等东说念主[159]从分治算法的角度， 建议了基于分类置信度排序的神经会聚鲁棒性考证方法， 将神经会聚鲁棒性考证问题转动到些许定向类型考证的子问题， 有用升迁了多个开源考证器具的鲁棒性证伪性能. 因此， 从不同的角度考证神经会聚的鲁棒性也会有很大的发展空间.
● 研究其他类型神经会聚的鲁棒性. 在大型的工业系统包括应用比较以前的神经会聚除了深度神经会聚和RNN以外还有CNN和图会聚等. 深度神经会聚的鲁棒性考证照旧有了比较丰富的研究， 但其他种类的会聚鲁棒性研究比较少， 仍然有很大的研究空间. Zhang等东说念主[160]建议了以Swish函数动作激活函数的神经会聚的鲁棒性考证方法， 他们利用线性贴近技艺将鲁棒性考证问题转动为管理求解问题， 并对非线性激活函数进行线性贴近， 进一步考证Swish神经会聚的鲁棒性. Zhang等东说念主[161]建议了一般量化神经会聚(quantized neural network， QNN) 的MILP建模方法， 并基于此想象了一般量化神经会聚鲁棒性分析框架， 实验驱散露馅比此前基于SMT的鲁棒性考证方法在效力上具有彰着的上风.
● 研究大型智能系统的安全性. 目下神经会聚被以前应用于安全攸关系统中， 举例自动驾驶， 飞机巡航限制等， 保证神经会聚组件的安全性或者鲁棒性并不及以保证通盘智能系统的安全性. 对智能系统合座的安全性研究照旧存在不少职责， 包括Dreossi等东说念主建议的VerifAI[162， 163]器具， Kazak利用深度神经会聚考证相关念念想， 建议了一种考证深度强化学习(deep reinforcement learning， DRL) 系统的考证器具Verily[80]， Zhou等东说念主为多智能体学习框架MFAC建议了一个鲁棒性教师框架RoMFAC[164]， 使其具有精采的对抗鲁棒性， 以偏激他的智能系统考证器具NNV[122]， Percemon[165]等， 对自动驾驶和无东说念主机的运行场景进行考证. 因此， 对此类智能系统的鲁棒性、安全性考证也有很大的发展空间.
9 结 语神经会聚的鲁棒性研究在式样化考证领域正处于快速发展的时期， 跟着越来越多的智能系统应用于现实生涯， 神经会聚的鲁棒性考证也将变得愈加进击. 固然FNN的鲁棒性研究职责琳琅满目， 然而目下的研究仍然停留在中等限制的会聚上考证精度与效力的量度白虎 女優， 而难以拓展到践诺应用中的大型神经会聚中. 何况除了局部鲁棒性， 全局鲁棒性和概率鲁棒性等其他鲁棒性质的考证职责目下还比较匮乏. 同期， 咱们对神经会聚的预计机制和道理仍然不甚了解， 难以将这些式样化的考证方法应用于工业界含有神经会聚等智能组件的大型智能系统中. RNN因为具有更复杂的结构， 研究其局部鲁棒性的职责目下仍比较少， 能考证的神经会聚限制仅包含几百上千个神经元. 本文分析了多数的FNN和RNN考证的相关著作， 目的是梳理FNN和RNN考证方法的发展近况， 并揭示两种神经会聚鲁棒性考证方法之间的内在筹商. 咱们在终末探讨了神经会聚的一些其他鲁棒性的界说与考证方法， 以及神经会聚鲁棒性考证领域在畴昔具有后劲的研究标的， 但愿可以进一步鞭策神经会聚鲁棒性考证的研究.